
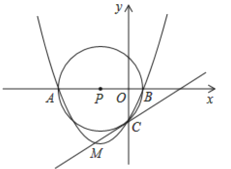
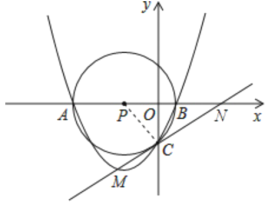
【题目】如图,在平面直角坐标系中,坐标原点为O,A点坐标为(-4,0),B点坐标为(1,0),以AB的中点P为圆心,AB为直径作⊙P与y轴的负半轴交于点C.
(1)求经过A、B、C三点的抛物线对应的函数表达式;
(2)设M为(1)中抛物线的顶点,试说明直线MC与⊙P的位置关系,并证明你的结论;
(3)在第二象限中是否存在的一点Q,使得以A,O,Q为顶点的三角形与△OBC相似.若存在,请求出所有满足的Q点坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)相切,见解析;(3)存在,(-4,8)、(-4,2)、
;(2)相切,见解析;(3)存在,(-4,8)、(-4,2)、![]() 、
、![]()
【解析】
(1)由A点坐标和B点坐标,可以求出AB的长度,即圆的直径可以求出,进而得出圆的半径长度,根据B点坐标,求出OP的长,再根据勾股定理求出C点坐标,设出二次函数交点式,将C点坐标代入求解即可.
(2)直线与圆的位置关系无非是相切或不相切,可连接PC,证PC是否与MC垂直即可.本题可先求出直线MC与x轴的交点N的坐标,然后分别求出PN,PC,CN的长,用勾股定理逆定理进行判断.
(3)△OBC与△AOQ相似,△OBC与△AQO相似,△OBC与△QAO相似,△OBC与△QOA相似,四种情况讨论根据三角形相似的性质列出关系式求解即可.
 y个
y个
(1)连接PC,.
∵A(-4,0),B(1,0)
∴AB=5,
∵P是AB的中点,且是![]() 的圆心
的圆心
∴PC=PA=2.5,OP=4-2.5=1.5.
∴![]()
∴C(0,-2).
设经过A.B.C三点的抛物线为
![]()
![]()
![]() .
.
抛物线为![]()
(2)直线MC与![]() 相切.
相切.
将![]() 配方,得
配方,得
![]()
∴顶点M为![]()
设直线MC为y=kx+b,则有
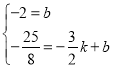
解得
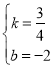
∴直线MC为![]()
设MC与x轴交于点N,
在![]() 中,令y=0,得
中,令y=0,得![]()
![]()
![]()
![]()
∴MC与OP相切.
(3)当△OBC与△AOQ相似,
OB:OC=AO:AQ,
即1:2=4:AQ,
解得AQ=8,
则Q点坐标为(-4,8);
当△OBC与△AQO相似,
OB:OC=AQ:AO,
即1:2=AQ:4,
解得AQ=2,
则Q点坐标为(-4,2);
当△OBC与△QAO相似,
OC:BC=QO:AO,
即![]() ,
,
解得![]() ,
,
则Q点横坐标为![]()
纵坐标为![]() .
.
则Q点坐标为![]()
当△OBC与△QO4相似,
OB:BC=QO:AO,
即![]() ,
,
解得![]() ,
,
则Q点横坐标为![]()
纵坐标为![]()
则Q点坐标为![]()
综上所述,使得以A,O,Q为顶点的三角形与△OBC相似,
所有满足的Q点坐标为:
(-4,8)、(-4,2)、![]() 、
、![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax![]() +bx+c的x,y的对应值如下表:
+bx+c的x,y的对应值如下表:
x | … | -1 |
| 0 |
| 1 |
| 2 | … |
y | … | -1 |
| m |
| 1 |
| n | … |
下列关于该函数性质的判断:①该二次函数有最大值;②当x>0时,函数y随x的增大而减小;③不等式y<﹣1的解集是﹣1<x<2;④关于x的一元二次方程ax2+bx+c=0的两个实数根分别位于﹣1<x<![]() 和
和![]() <x<2之间.其中正确结论的个数有( )
<x<2之间.其中正确结论的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新罗区某校元旦文艺汇演,需要从3名女生和1名男生中随机选择主持人.
(1)如果选择1名主持人,那么男生当选的概率是多少?
(2)如果选择2名主持人,用画树状图(或列表)求出2名主持人恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有三个分别写有数字6,-2,7的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树状图的方法,求下列事件的概率:
(1)两次取出小球上的数字相同;
(2)两次取出小球上的数字之和大于10.
查看答案和解析>>
科目:初中数学 来源: 题型:
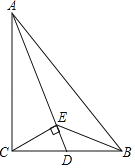
【题目】如图,在Rt△ABC中,∠ACB=90°,点D是边BC的中点,联结AD.过点C作CE⊥AD于点E,联结BE.
(1)求证:BD2=DEAD;
(2)如果∠ABC=∠DCE,求证:BDCE=BEDE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=﹣x+n的图象与反比例函数y=![]() 的图象交于A(4,﹣2),B(﹣2,m)两点.
的图象交于A(4,﹣2),B(﹣2,m)两点.
(1)请直接写出不等式﹣x+n≤![]() 的解集;
的解集;
(2)求反比例函数和一次函数的解析式;
(3)过点A作x轴的垂线,垂足为C,连接BC,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.以下说法错误的是

A.加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系是y=﹣8t+25
B.途中加油21升
C.汽车加油后还可行驶4小时
D.汽车到达乙地时油箱中还余油6升
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com