
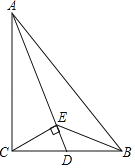
【题目】如图,在Rt△ABC中,∠ACB=90°,点D是边BC的中点,联结AD.过点C作CE⊥AD于点E,联结BE.
(1)求证:BD2=DEAD;
(2)如果∠ABC=∠DCE,求证:BDCE=BEDE.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)证明△CDE∽△ADC推出![]() ,可得CD2=DEDA即可解决问题.
,可得CD2=DEDA即可解决问题.
(2)利用相似三角形的性质首先证明AC=BE,再证明△ACE∽△CDE,可得![]() ,可得
,可得![]() 即可解决问题.
即可解决问题.
解:
(1)证明:如图1中,

∵CE⊥AD,
∴∠CED=∠ACD=90![]() ,
,
∵∠CDE=∠ADC,
∴△CDE∽△ADC
∴![]() ,
,
∴CD2=DEDA,
∵DB=CD,
∴∴BD2=DEDA.
(2)解:如图2中,

∵BD2=DEDA,
∴![]() ,
,
∵∠CDE=∠ADB,
∴△BDE∽△ADB,
∴∠DEB=∠ABC,
∵∠ABD=∠ECD,
∴∠BED=∠BCE,
∵∠EBD=∠CBE,
∴△EBD∽△CBE,
∴![]() ,
,
∴BE2=BDBC,
∵CD=BD,
∴BE2=2CD2,
∵∠DCE+∠ACE=90![]() ,∠CAD+∠ACE=90
,∠CAD+∠ACE=90![]() ,
,
∴∠CAD=∠ECD=∠ABC,
∵∠ACD=∠BCA,
∴△ACD∽△BCA,
∴![]() ,
,
∴AC2=CDCB=2CD2,
∴AC=BE,
∵△ACE∽△CDE,
∴![]() ,
,
∴![]() ,
,
∴BDCE=BEDE.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD延长线交于点F,且∠AFB=∠ABC.
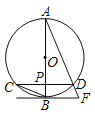
(1)求证:直线BF是⊙O的切线;
(2)若CD=2![]() ,BP=1,求⊙O的半径.
,BP=1,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
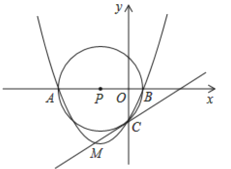
【题目】如图,在平面直角坐标系中,坐标原点为O,A点坐标为(-4,0),B点坐标为(1,0),以AB的中点P为圆心,AB为直径作⊙P与y轴的负半轴交于点C.
(1)求经过A、B、C三点的抛物线对应的函数表达式;
(2)设M为(1)中抛物线的顶点,试说明直线MC与⊙P的位置关系,并证明你的结论;
(3)在第二象限中是否存在的一点Q,使得以A,O,Q为顶点的三角形与△OBC相似.若存在,请求出所有满足的Q点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
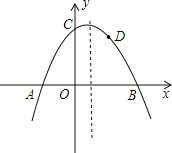
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
(1)求抛物线的解析式.
(2)若点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标,若不存在,请说明理由.
注:二次函数![]() (
(![]() ≠0)的对称轴是直线
≠0)的对称轴是直线![]() =
=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
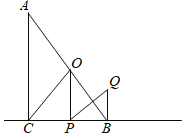
【题目】如图所示,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与B、C重合),连接OC、OP,将OP绕点P顺时针旋转60°,得到线段PQ,连接BQ,若∠BPO=15°,BP=4,则BQ的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
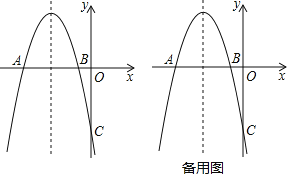
【题目】如图所示,抛物线y=ax2+bx+c与x轴交于A、B两点,A(﹣5,0),与y轴交于C(0,﹣5),并且对称轴x=﹣3.
(1)求抛物线的解析式;
(2)P在x轴上方的抛物线上,过P的直线y=x+m与直线AC交于点M,与y轴交于点N,求PM+MN的最大值;
(3)点D为抛物线对称轴上一点,
①当△ACD是以AC为直角边的直角三角形时,求D点坐标;
②若△ACD是锐角三角形,求点D的纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
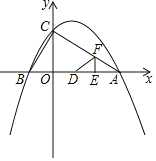
【题目】综合与探究:
已知二次函数y=﹣![]() x2+
x2+![]() x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)求证:△ABC为直角三角形;
(3)如图,动点E,F同时从点A出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒![]() 个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
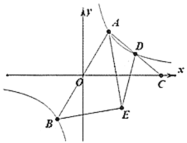
【题目】如图,过原点的直线与反比例函数![]() (
(![]() )的图象交于
)的图象交于![]() ,
,![]() 两点,点
两点,点![]() 在第一象限.点
在第一象限.点![]() 在
在![]() 轴正半轴上,连结
轴正半轴上,连结![]() 交反比例函数图象于点
交反比例函数图象于点![]() .
.![]() 为
为![]() 的平分线,过点
的平分线,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,连结
,连结![]() .若
.若![]() 是线段
是线段![]() 中点,
中点,![]() 的面积为4,则
的面积为4,则![]() 的值为______.
的值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com