
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD延长线交于点F,且∠AFB=∠ABC.
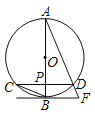
(1)求证:直线BF是⊙O的切线;
(2)若CD=2![]() ,BP=1,求⊙O的半径.
,BP=1,求⊙O的半径.
【答案】(1)见解析;(2)3
【解析】
(1)由圆周角定理得出∠ABC=∠ADC,由已知得出∠ADC=∠AFB,证出CD∥BF,得出AB⊥BF,即可得出结论;
(2)设⊙O的半径为r,连接OD.由垂径定理得出PD=PC=![]() CD=
CD=![]() ,得出OP=r-1在Rt△OPD中,由勾股定理得出方程,解方程即可.
,得出OP=r-1在Rt△OPD中,由勾股定理得出方程,解方程即可.
解:(1)证明:∵弧AC=弧AC,
∴∠ABC=∠ADC,
∵∠AFB=∠ABC,
∴∠ADC=∠AFB,
∴CD∥BF,
∵CD⊥AB,
∴AB⊥BF,
∵AB是圆的直径,
∴直线BF是⊙O的切线;
(2)解:设⊙O的半径为r,连接OD.如图所示:
∵AB⊥BF,CD=2![]() ,
,
∴PD=PC=![]() CD=
CD=![]() ,
,
∵BP=1,
∴OP=r﹣1
在Rt△OPD中,由勾股定理得:r2 =(r﹣1)2+(![]() )2
)2
解得:r=3.
即⊙O的半径为3.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某中学围绕“哈尔滨市周边五大名山,即:香炉山、凤凰山、金龙山、帽儿山、二龙山,你最喜欢那一座山?(每名学生必选且只选一座山)的问题在全校范围内随机抽取了部分学生进行问卷调查,根据调查结果绘制了如图的不完整的统计图:
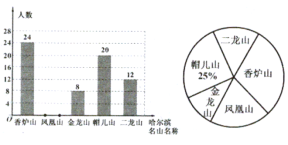
(1)求本次调查的样本容量;
(2)求本次调查中,最喜欢凤凰山的学生人数,并补全条形统计图;
(3)若该中学共有学生1200人,请你估计该中学最喜欢香炉山的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
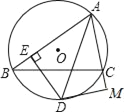
【题目】如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC于M.
(1)求证:BE=CM.
(2)求证:AB﹣AC=2BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax![]() +bx+c的x,y的对应值如下表:
+bx+c的x,y的对应值如下表:
x | … | -1 |
| 0 |
| 1 |
| 2 | … |
y | … | -1 |
| m |
| 1 |
| n | … |
下列关于该函数性质的判断:①该二次函数有最大值;②当x>0时,函数y随x的增大而减小;③不等式y<﹣1的解集是﹣1<x<2;④关于x的一元二次方程ax2+bx+c=0的两个实数根分别位于﹣1<x<![]() 和
和![]() <x<2之间.其中正确结论的个数有( )
<x<2之间.其中正确结论的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC的顶角∠A=36°,若将其绕点C顺时针旋转36°,得到△![]() ,点B′在AB边上,
,点B′在AB边上,![]() 交AC于E,连接AA′.有下列结论:①△ABC≌△
交AC于E,连接AA′.有下列结论:①△ABC≌△![]() ;②四边形
;②四边形![]() 是平行四边形;③图中所有的三角形都是等腰三角形;其中正确的结论是( )
是平行四边形;③图中所有的三角形都是等腰三角形;其中正确的结论是( )
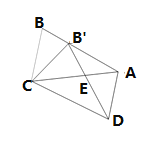
A.①②B.① ③C.②③D.① ② ③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新罗区某校元旦文艺汇演,需要从3名女生和1名男生中随机选择主持人.
(1)如果选择1名主持人,那么男生当选的概率是多少?
(2)如果选择2名主持人,用画树状图(或列表)求出2名主持人恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
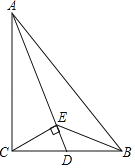
【题目】如图,在Rt△ABC中,∠ACB=90°,点D是边BC的中点,联结AD.过点C作CE⊥AD于点E,联结BE.
(1)求证:BD2=DEAD;
(2)如果∠ABC=∠DCE,求证:BDCE=BEDE.
查看答案和解析>>
科目:初中数学 来源: 题型:
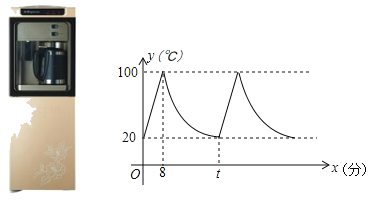
【题目】小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热(此过程中水温y(℃)与开机时间x(分)满足一次函数关系),当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系,当水温降至20C时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明上午八点将饮水机在通电开机(此时饮水机中原有水的温度为20℃后即外出散步,预计上午八点半散步回到家中,回到家时,他能喝到饮水机内不低于30℃的水吗?请说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com