
【题目】综合与探究:
已知二次函数y=﹣![]() x2+
x2+![]() x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)求证:△ABC为直角三角形;
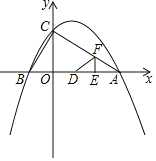
(3)如图,动点E,F同时从点A出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒![]() 个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
【答案】(1)点A的坐标为(4,0),点B的坐标为(﹣1,0),点C的坐标为(0,2);(2)证明见解析;(3)t=![]() .
.
【解析】
(1)利用x=0和y=0解方程即可求出A、B、C三点坐标;
(2)先计算△ABC的三边长,根据勾股定理的逆定理可得结论;
(3)先证明△AEF∽△ACB,得∠AEF=∠ACB=90°,确定△AEF沿EF翻折后,点A落在x轴上点D处,根据△DCO≌△BCO时,BO=OD,列方程4-4t=1,可得结论.
(1)解:当y=0时,﹣![]() x+2=0,
x+2=0,
解得:x1=1,x2=4,
∴点A的坐标为(4,0),点B的坐标为(﹣1,0),
当x=0时,y=2,
∴点C的坐标为(0,2);
(2)证明:∵A(4,0),B(﹣1,0),C(0,2),
∴OA=4,OB=1,OC=2.
∴AB=5,AC=![]() =
=![]() ,
,
∴AC2+BC2=25=AB2,
∴△ABC为直角三角形;
(3)解:由(2)可知△ABC为直角三角形.且∠ACB=90°,
∵AE=2t,AF=![]() t,
t,
∴![]() ,
,
又∵∠EAF=∠CAB,
∴△AEF∽△ACB,
∴∠AEF=∠ACB=90°,
∴△AEF沿EF翻折后,点A落在x轴上点 D处,
由翻折知,DE=AE,
∴AD=2AE=4t,
当△DCO≌△BCO时,BO=OD,
∵OD=4﹣4t,BO=1,
∴4﹣4t=1,t=![]() ,
,
即:当t=![]() 秒时,△DCO≌△BCO.
秒时,△DCO≌△BCO.


科目:初中数学 来源: 题型:
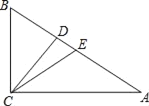
【题目】如图,在Rt△ABC中,CD,CE分别是斜边AB上的高,中线,BC=a,AC=b.
(1)若a=3,b=4,求DE的长;
(2)直接写出:CD= (用含a,b的代数式表示);
(3)若b=3,tan∠DCE=![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
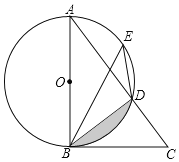
【题目】 如图,AB是⊙O的直径,点E是AD上的一点,∠DBC=∠BED
(1)求证:BC是⊙O的切线;
(2)已知AD=3,CD=1,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线x=-1的抛物线y=a(x-h)![]() -4(a≠0)与x轴相交于A、B两点,与y轴交于点C,其中点A的坐标为(-3,0).
-4(a≠0)与x轴相交于A、B两点,与y轴交于点C,其中点A的坐标为(-3,0).
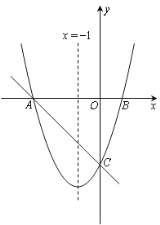
(1)求该抛物线的解析式;
(2)若点P在抛物线上,且S△POC=4S△BOC.求点P的坐标;
(3)设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点.
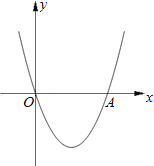
(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;
(3)对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a和b,定义新运算“@”:a@b=![]()
(1)计算20182018@(8@28)的值;
(2)若(x﹣1)@(3﹣2x)=2,求实数x的值;
(3)设函数y1=(2﹣x2)@(4x﹣x2),若函数y2=y1﹣m的图象与x轴恰有两个交点,求实数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“双十一购物狂欢节”来临之际,某超市拟举办购物促销活动,从分店调动了20名店员参与总店活动,其中男店员8人,女店员12人.

(1)若从这20人中随机选取一人作为宣传人员,求选到女店员的概率;
(2)分店的某活动中需要甲、乙两店员中选一人参与,他们准备以游戏的方式决定由谁参加,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲参加,否则乙参加,请用树状图或列表法分别求出甲、乙两人参加这项活动的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com