
����Ŀ����˫ʮһ����ڡ�����֮�ʣ�ij������ٰ칺���������ӷֵ������20����Ա�����ܵ��������е�Ա8�ˣ�Ů��Ա12��.

��1��������20�������ѡȡһ����Ϊ������Ա����ѡ��Ů��Ա�ĸ��ʣ�
��2���ֵ��ij�����Ҫ�ס�������Ա��ѡһ�˲��룬����������Ϸ�ķ�ʽ������˭�μӣ���Ϸ�������£��������������ֱַ�Ϊ2��3��4��5���˿���ϴ�Ⱥ����ֳ��·������棬������ȡ2�ţ�����������֮��Ϊż������ײμӣ������Ҳμӣ�������״ͼ���б����ֱ�����ס������˲μ������ĸ���.
���𰸡���1��![]() .��2���ײμ������ĸ���Ϊ
.��2���ײμ������ĸ���Ϊ![]() ���Ҳμӻ�ĸ���Ϊ
���Ҳμӻ�ĸ���Ϊ![]() .
.
��������
(1)ֱ�����ø��ʹ�ʽ������ɣ���2��������״ͼ��ʾ�����п��ܽ������ø��ʹ�ʽ��⼴��.
��1���ߴӷֵ������20����Ա�����ܵ��������е�Ա8�ˣ�Ů��Ա12�ˣ�
�����ѡȡһ����Ϊ������Ա��ѡ��Ů��Ա�ĸ���Ϊ![]() .
.
��2������״ͼ����
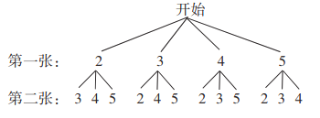
��������֮�ͷֱ�Ϊ5��6��7��5��7��8��6��7��9��7��8��9����12��������õ�ÿ������Ŀ�������ͬ.
����ż��Ϊ4��.
��õ�ż���ĸ���Ϊ![]() .
.
��õ������ĸ���Ϊ![]() .
.
��ײμ������ĸ���Ϊ![]() ���Ҳμӻ�ĸ���Ϊ
���Ҳμӻ�ĸ���Ϊ![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽����
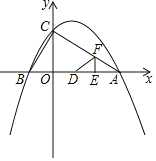
��֪���κ���y����![]() x2+
x2+![]() x+2��ͼ����x�ύ��A��B���㣨��B�ڵ�A����ࣩ����y�ύ�ڵ�C��
x+2��ͼ����x�ύ��A��B���㣨��B�ڵ�A����ࣩ����y�ύ�ڵ�C��
��1�����A��B��C�����ꣻ
��2����֤����ABCΪֱ�������Σ�
��3����ͼ������E��Fͬʱ�ӵ�A���������е�E��ÿ��2����λ���ȵ��ٶ���AB�����յ�B�˶�����F��ÿ��![]() ����λ���ȵ��ٶ�������AC�����˶�������Fֹͣ�˶�ʱ����E��ֹ֮ͣ�˶������˶�ʱ��Ϊt�룬����EF������AEF��EF���ۣ�ʹ��A���ڵ�D�����õ���DEF������F��AC��ʱ���Ƿ����ijһʱ��t��ʹ����DCO�ա�BCO������D�����B�غϣ������ڣ����t��ֵ���������ڣ���˵�����ɣ�
����λ���ȵ��ٶ�������AC�����˶�������Fֹͣ�˶�ʱ����E��ֹ֮ͣ�˶������˶�ʱ��Ϊt�룬����EF������AEF��EF���ۣ�ʹ��A���ڵ�D�����õ���DEF������F��AC��ʱ���Ƿ����ijһʱ��t��ʹ����DCO�ա�BCO������D�����B�غϣ������ڣ����t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
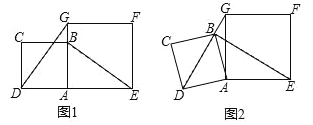
����Ŀ��������ABCD��������AEFG�ı߳��ֱ�Ϊ2��![]() ����B�ڱ�AG������D���߶�EA���ӳ�����������BE��
����B�ڱ�AG������D���߶�EA���ӳ�����������BE��
��1����ͼ1����֤��DG��BE��
��2����ͼ2����������ABCD�Ƶ�A����ʱ�뷽����ת������Bǡ�������߶�DG��ʱ�����߶�BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ���ѧ�����շ�չ�����ز����������ڲ������ɵ��������ĸ߶ȣ����磬ͨ�����в���ɲ���ɽ�ĸ߶�PQ(��ͼ)��
��1����������ˮƽ���ϵ�A������һ����ͣ�������QA�����ߵ�M�������ɽ��P����Ͷ���B��M��һ��ֱ���ϣ�
��2�������������������QA�ϵ�C������ԭ��������ߵ�N�������ɽ��P����Ͷ���D��N��һ��ֱ���ϣ�
��3���������AM��CN�ij��ֱ�Ϊ![]() ��a1��a2���ɵù�ʽ��PQ��
��a1��a2���ɵù�ʽ��PQ��![]() ��
��![]() .��������ʽ�У�d��ʾ���ǣ� ��
.��������ʽ�У�d��ʾ���ǣ� ��
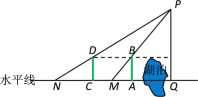
A. QA�ij� B. AC�ij� C. MN�ij� D. QC�ij�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ����OABC����ֱ������ϵ�У�OΪ����ԭ�㣬��A��y���������ϣ���E�DZ�AB�ϵ�һ������![]() �����A��B�غ�
�����A��B�غ�![]() ������E�ķ���������
������E�ķ���������![]() ��ͼ�����BC���ڵ�F
��ͼ�����BC���ڵ�F
![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ����k��ֵ��
����k��ֵ��
![]() ��
��![]() ��
��![]() ������������
������������![]() ��ͼ�����AB����BC���ڵ�E��F����
��ͼ�����AB����BC���ڵ�E��F����![]() ��EF�۵�����Bǡ������OC�ϣ���k��ֵ��
��EF�۵�����Bǡ������OC�ϣ���k��ֵ��
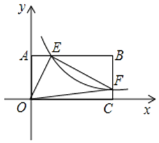
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB = 90����BC = 6��AC = 8����D��AB����һ�㣬����D��DE // BC������AC��E������C��CF // AB����DE���ӳ����ڵ�F��
��1�����![]() �����߶�EF�ij���
�����߶�EF�ij���
��2�����CFE������ֵ��
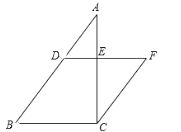
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������ABC�У���D��E�ֱ��ڱ�AC��AB�ϣ�AG��BC�ڵ�G��AF��DE�ڵ�F����EAF=��GAC��
��1����֤����ADE�ס�ABC��
��2����AF=3��AG=5������ADE����ABC���ܳ�֮�ȣ�
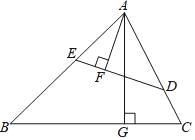
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��D��E�ֱ��ǡ�O�����뾶OA��OB���е㣬![]() ��
��
��1����֤��CD=CE��
��2������AOB=120�㣬OA=x���ı���ODCE�����Ϊy����y��x�ĺ�����ϵʽ��
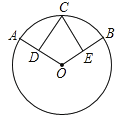
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����κ���C1��y1��ax2+2ax+a��1(a��0)
(1)�Ѷ��κ���C1�ı���ʽ����y��a(x��h)2+b(a��0)����ʽ����д���������ꣻ
(2)��֪���κ���C1��ͼ����A(��3��1)��
����a��ֵ��
����B�ڶ��κ���C1��ͼ���ϣ���A��B���ڶԳ���Գƣ�����AB�����κ���C2��y2��kx2+kx(k��0)��ͼ�����߶�ABֻ��һ�����㣬��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com