
����Ŀ����֪�����κ���C1��y1��ax2+2ax+a��1(a��0)
(1)�Ѷ��κ���C1�ı���ʽ����y��a(x��h)2+b(a��0)����ʽ����д���������ꣻ
(2)��֪���κ���C1��ͼ����A(��3��1)��
����a��ֵ��
����B�ڶ��κ���C1��ͼ���ϣ���A��B���ڶԳ���Գƣ�����AB�����κ���C2��y2��kx2+kx(k��0)��ͼ�����߶�ABֻ��һ�����㣬��k��ȡֵ��Χ��
���𰸡�(1)y1��a(x+1)2��1������Ϊ(��1����1)��(2)��![]() ����k��ȡֵ��Χ��
����k��ȡֵ��Χ��![]() ��k��
��k��![]() ��k����4��
��k����4��
��������
(1)���ɶ���ʽ������ã�
(2)���ѵ�A(��3��1)������κ���C1��y1��ax2+2ax+a��1�������a��ֵ��
�����ݶԳƵ����ʵó�B�����꣬Ȼ�������������ۼ�����ã�
(1)y1��ax2+2ax+a��1��a(x+1)2��1��
�ඥ��Ϊ(��1����1)��
(2)���߶��κ���C1��ͼ����A(��3��1)��
��a(��3+1)2��1��1��
��a��![]() ��
��
����A(��3��1)���Գ���Ϊֱ��x����1��
��B(1��1)��
��k��0ʱ��
���κ���C2��y2��kx2+kx(k��0)��ͼ��A(��3��1)ʱ��1��9k��3k�����k��![]() ��
��
���κ���C2��y2��kx2+kx(k��0)��ͼ��B(1��1)ʱ��1��k+k�����k��![]() ��
��
��![]() ��k��
��k��![]() ��
��
��k��0ʱ���߶��κ���C2��y2��kx2+kx��k(x+![]() )2��
)2��![]() k��
k��
�ੁ![]() k��1��
k��1��
��k����4��
���ϣ����κ���C2��y2��kx2+kx(k��0)��ͼ�����߶�ABֻ��һ�����㣬k��ȡֵ��Χ��![]() ��k��
��k��![]() ��k����4��
��k����4��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˫ʮһ����ڡ�����֮�ʣ�ij������ٰ칺���������ӷֵ������20����Ա�����ܵ��������е�Ա8�ˣ�Ů��Ա12��.

��1��������20�������ѡȡһ����Ϊ������Ա����ѡ��Ů��Ա�ĸ��ʣ�
��2���ֵ��ij�����Ҫ�ס�������Ա��ѡһ�˲��룬����������Ϸ�ķ�ʽ������˭�μӣ���Ϸ�������£��������������ֱַ�Ϊ2��3��4��5���˿���ϴ�Ⱥ����ֳ��·������棬������ȡ2�ţ�����������֮��Ϊż������ײμӣ������Ҳμӣ�������״ͼ���б����ֱ�����ס������˲μ������ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⷢ�֣�
��![]() ����ͼ�٣�
����ͼ�٣�![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��������һ�㣬��
��������һ�㣬��![]() ����СֵΪ__________��
����СֵΪ__________��
��![]() ����ͼ�ڣ�����
����ͼ�ڣ�����![]() �У�
��![]() ��
��![]() ����
����![]() ����
����![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ���
�ϣ���![]() ����Сֵ��
����Сֵ��
��![]() ����ͼ�ۣ�����
����ͼ�ۣ�����![]() �У�
��![]() ��
��![]() ����
����![]() ��
��![]() ����һ�㣬��
����һ�㣬��![]() ����
����![]() ��
��![]() ���ϵ�����һ�㣬��
���ϵ�����һ�㣬��![]() ��
��![]() ���ۣ���
���ۣ���![]() �Ķ�Ӧ��Ϊ��
�Ķ�Ӧ��Ϊ��![]() ������
������![]() ��
��![]() ���ı���
���ı���![]() ������Ƿ������Сֵ�������ڣ��������Сֵ����ʱ
������Ƿ������Сֵ�������ڣ��������Сֵ����ʱ![]() �ij��ȣ��������ڣ���˵�����ɣ�
�ij��ȣ��������ڣ���˵�����ɣ�



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й�������������ӱ��۰���������һ�ش��ʩ�ؽ����������ܱ����������ˮƽ��չ��ͬʱҲ����������̻���ijˮ���������ڵ�һ�ܹ���һ��ˮ��1160����Ԥ���ڵڶ��ܽ��������������۸�Ϊÿ��10Ԫ�����ۼ�Ϊÿ��12Ԫ�����ȫ���۳������ۼ�ÿ�Ǽ�0.1Ԫ�������ͼ���2����
��1�����þ������ڵڶ��ܵ�����������1100�������ۼ�Ӧ�����ڶ���Ԫ��
��2�����������Ϻã�������ˮ�����۱ȵ�һ��ÿ��������20%���þ����������˽�����������ǿ���������ȣ���������ܵ������ȵڶ����ڣ�1�������µ��������������m%�����ۼ۱ȵڶ����ڣ�1�������µ�����ۼۼ�����![]() m%���������������ﵽ3388Ԫ����m��ֵ��m��10����
m%���������������ﵽ3388Ԫ����m��ֵ��m��10����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�����ѧ���ϣ���ʦ����������⣺
�߹���ͼ����Բ��һ����Բ�����ߣ�
��֪����O�͵�P
�����P����O������
С������Ҫ�������£�
��ͼ����1������OP�����߶�OP���е�A��
��2����AΪԲ�ģ�OA��Ϊ�뾶��Բ������O�ڵ�B��C��
��3����ֱ��PB��PC��
����PB��PC������������ߣ�
��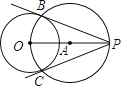
��ʦ˵����С����������ȷ�ģ���
��ش�С������ͼ������_____��
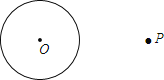
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��ת�̣�ת�̷ֳ�8����ͬ��ͼ�Σ���ɫ��Ϊ�졢�̡������֣�ָ���λ�ù̶���ת��ת�̺���������ֹͣ�����е�ij�����λ�ǡ��ͣ��ָ����ָ��λ��(ָ��ָ������ͼ�εĽ���ʱ������ָ���ұߵ�ͼ��)���������¼��ĸ��ʣ�
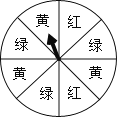
��1��ָ��ָ���ɫ��
��2��ָ��ָ���ɫ����ɫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽����о�����ˮ�������ijС����������20����ͥ��������Щ��ͥ������ˮ������ͳ�ƣ�������±���
����ˮ�����֣� | 4 | 5 | 6 | 8 | 13 |
���� | 4 | 5 | 7 | 3 | 1 |
�������20����ͥ������ˮ��������˵����ȷ���ǣ�������
A.��λ����5B.ƽ������5C.������6D.������6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
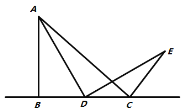
����Ŀ�������ⱳ������ͼ1��ʾ����![]() �У�
��![]() ��
��![]() ����DΪֱ��
����DΪֱ��![]() �ϵĸ����㣨����B��C�غϣ�������
�ϵĸ����㣨����B��C�غϣ�������![]() �����߶�
�����߶�![]() �Ƶ�D��˳ʱ�뷽����ת90����ʹ��A��ת����E������
�Ƶ�D��˳ʱ�뷽����ת90����ʹ��A��ת����E������![]() .
.
�������̽�������D���߶�![]() ���˶���ͨ���۲졢������С���γ������µĽ���˼·������E��
���˶���ͨ���۲졢������С���γ������µĽ���˼·������E��![]() ��ֱ��
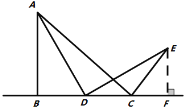
��ֱ��![]() ��F����ͼ2��ʾ��ͨ��֤��
��F����ͼ2��ʾ��ͨ��֤��![]() ______������֤
______������֤![]() ��_____�����Σ��Ӷ����
��_____�����Σ��Ӷ����![]() ______��.
______��.
������̽���������D���߶�![]() ���ӳ������˶�����ͼ3��ʾ�����
���ӳ������˶�����ͼ3��ʾ�����![]() �Ķ���.
�Ķ���.
����չ���죩����![]() ������D��ֱ��
������D��ֱ��![]() ���˶�ʱ����
���˶�ʱ����![]() ����ֱ��д��
����ֱ��д��![]() ����Сֵ.
����Сֵ.
ͼ1 ͼ2 ͼ3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
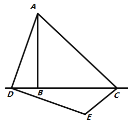
����Ŀ�����ǽ�����ȫ����ijƽ��ͼ�ε���СԲ��Ϊ��ƽ��ͼ�ε���С����Բ�������߶�AB����С����Բ�������߶�ABΪֱ����Բ��

��1����ֱ�������ͼ�����������ε���С����Բ��Ҫ���ó߹���ͼ��������ͼ�ۼ�����д��������
��2��̽�������ε���С����Բ�кι��ɣ���д�������õ��Ľ��ۣ���Ҫ��֤������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com