练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆．例如线段AB的最小覆盖圆就是以线段AB为直径的圆．

    （1）请分别作出下图中两个三角形的最小覆盖圆（要求用尺规作图，保留作图痕迹，不写作法）；

    （2）探究三角形的最小覆盖圆有何规律？请写出你所得到的结论（不要求证明）．

    【答案】(1)见解析;(2) 锐角三角形（和直角三角形）的最小覆盖圆是其外接圆；钝角三角形的最小覆盖圆是以其最长边为直径的圆

    【解析】

    第一个三角形是锐角三角形，那么它的最小覆盖圆应该是三角形ABC的外接圆；
    第二个三角形是钝角三角形，那么它的最小覆盖圆应该是以BC为直径的圆．

    解：（1）如图；

    （2）锐角三角形（和直角三角形）的最小覆盖圆是其外接圆；钝角三角形的最小覆盖圆是以其最长边为直径的圆；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：二次函数C1：y1＝ax2+2ax+a﹣1(a≠0)

    (1)把二次函数C1的表达式化成y＝a(x﹣h)2+b(a≠0)的形式，并写出顶点坐标；

    (2)已知二次函数C1的图象经过点A(﹣3，1)．

    ①求a的值；

    ②点B在二次函数C1的图象上，点A，B关于对称轴对称，连接AB．二次函数C2：y2＝kx2+kx(k≠0)的图象，与线段AB只有一个交点，求k的取值范围．

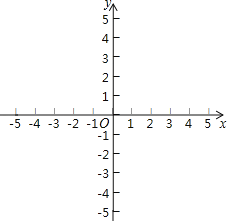
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD是正方形，△ADF旋转一定角度后得到△ABE，且点E在线段AD上，若AF=4，∠F=60°．

    （1）指出旋转中心和旋转角度；

    （2）求DE的长度和∠EBD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是(，称为黄金比例)，如图，著名的“断臂维纳斯”便是如此，此外，最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是，若某人的身材满足上述两个黄金比例，且头顶至咽喉的长度为，则其升高可能是( )

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

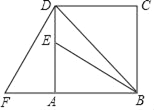
    【题目】如图，△ABC中，∠ACB=72°，将△ABC绕点B按逆时针方向旋转得到△BDE（点D与点 A是对应点，点E与点C是对应点），且边DE恰好经过点C，则∠ABD的度数为

    A. 36° B. 40° C. 45° D. 50°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

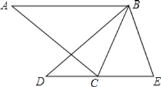
    【题目】（1）解方程：x2﹣5x﹣6＝0

    （2）如图，△ABC中∠C＝90°

    ①将△ABC绕A点逆时针旋转90°，画出旋转后的三角形△AB′C′；

    ②若BC＝3，AC＝4，B点旋转后的对应是B′，求 的长

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在正方形ABCD中，G为CD边中点，连接AG并延长交BC边的延长线于E点，对角线BD交AG于F点．已知FG＝2，则线段AE的长度为_____．

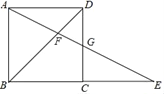
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，ABCD为矩形纸片，E、F分别为AB、DC上的点，将此矩形两次翻折，RM和FN为折痕，其中、分别为A、D的对应点；且点在射线EF上；、分别为B、C的对应点，且点在射线FE上.

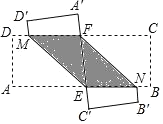
    （1）求证：四边形ENFM为平行四边形；

    （2）若四边形ENFM为菱形，求∠EMF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知点E为正方形ABCD对角线CA延长线上一点，过E点作EF⊥CB交其延长线于点F，且EF＝4，AC＝

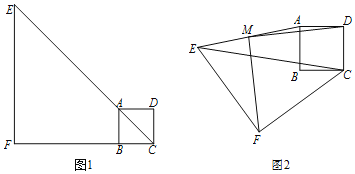
    （1）如图1，连接BE，求线段BE的长；

    （2）将等腰Rt△CEF绕C点旋转至如图2的位置，连接AE，M点为AE的中点，连接MD、MF，求MD与MF的关系；

    （3）将△CEF绕C点旋转一周，请直接写出点M在这个过程中的运动路径长为　 　．

    查看答案和解析>>

    同步练习册答案