
【题目】如图,ABCD为矩形纸片,E、F分别为AB、DC上的点,将此矩形两次翻折,RM和FN为折痕,其中![]() 、
、![]() 分别为A、D的对应点;且点
分别为A、D的对应点;且点![]() 在射线EF上;
在射线EF上;![]() 、
、![]() 分别为B、C的对应点,且点
分别为B、C的对应点,且点![]() 在射线FE上.
在射线FE上.
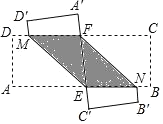
(1)求证:四边形ENFM为平行四边形;
(2)若四边形ENFM为菱形,求∠EMF的度数.
 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】(问题背景)如图1所示,在![]() 中,
中,![]() ,
,![]() ,点D为直线
,点D为直线![]() 上的个动点(不与B、C重合),连结
上的个动点(不与B、C重合),连结![]() ,将线段
,将线段![]() 绕点D按顺时针方向旋转90°,使点A旋转到点E,连结
绕点D按顺时针方向旋转90°,使点A旋转到点E,连结![]() .
.
(问题初探)如果点D在线段![]() 上运动,通过观察、交流,小明形成了以下的解题思路:过点E作
上运动,通过观察、交流,小明形成了以下的解题思路:过点E作![]() 交直线
交直线![]() 于F,如图2所示,通过证明
于F,如图2所示,通过证明![]() ______,可推证
______,可推证![]() 是_____三角形,从而求得
是_____三角形,从而求得![]() ______°.
______°.
(继续探究)如果点D在线段![]() 的延长线上运动,如图3所示,求出
的延长线上运动,如图3所示,求出![]() 的度数.
的度数.
(拓展延伸)连接![]() ,当点D在直线
,当点D在直线![]() 上运动时,若
上运动时,若![]() ,请直接写出
,请直接写出![]() 的最小值.
的最小值.
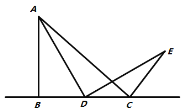
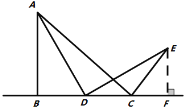
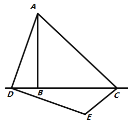
图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段AB的最小覆盖圆就是以线段AB为直径的圆.

(1)请分别作出下图中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
(2)探究三角形的最小覆盖圆有何规律?请写出你所得到的结论(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
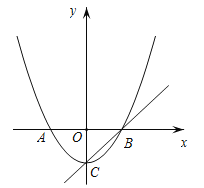
【题目】如图,已知顶点为![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,直线
两点,直线![]() 过顶点
过顶点![]() 和点
和点![]() .
.
(1)求![]() 的值;
的值;
(2)求函数![]() 的解析式;
的解析式;
(3)抛物线上是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在边BC,CD上,且BE=CF.连接AE,BF,AE与BF交于点G.下列结论错误的是( )
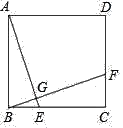
A. AE=BF B. ∠DAE=∠BFC
C. ∠AEB+∠BFC=90° D. AE⊥BF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:任何有理数的平方都是一个非负数,即对于任何有理数a,都有![]() 成立,所以,当
成立,所以,当![]() 时,
时,![]() 有最小值0.
有最小值0.
(应用):(1)代数式![]() 有最小值时,
有最小值时,![]() ;
;
(2)代数式![]() 的最小值是 ;
的最小值是 ;
(探究):求代数式![]() 的最小值,小明是这样做的:
的最小值,小明是这样做的:
![]()
![]()
![]()
∴当![]() 时,代数式
时,代数式![]() 有最小值,最小值为5.
有最小值,最小值为5.
(3)请你参照小明的方法,求代数式![]() 的最小值,并求此时a的值.
的最小值,并求此时a的值.
(拓展):(4)若![]() ,直接写出y的取值范围.
,直接写出y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
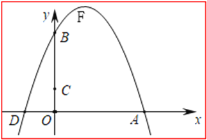
【题目】抛物线![]() 与y轴交于B,与x轴交于点D、A,点A在点D的右边,顶点为F,
与y轴交于B,与x轴交于点D、A,点A在点D的右边,顶点为F,![]()
(1)直接写出点B、A、F的坐标;
(2)设Q在该抛物线上,且![]() ,求点Q的坐标;
,求点Q的坐标;
(3)对大于1常数m,在x轴上是否存在点M,使得![]() ?若存在,求出点M坐标;若不存在,说明理由?
?若存在,求出点M坐标;若不存在,说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省南部的南宫山景区,为吸引游客组团来此旅游特推出了如下门票收费标准:
标准一:如果人数不超过20人,门票价格70元/人
标准二:如果人数超过20人,每超过1人,门票价格降低2元,但门票价格不低于55元/人
(1)若某单位组织22名员工去南宫山景区旅游,则购买门票共需多少元?
(2)若某单位共支付南宫山景区门票费用1500元,试求该单位这次共有多少名员工去南宫山旅游.
查看答案和解析>>
科目:初中数学 来源: 题型:
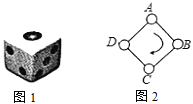
【题目】如图1,一枚质地均匀的正六面体骰子的六个面分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,如图2,正方形
,如图2,正方形![]() 的顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子朝上的那面上的数字是几,就沿正方形的边按顺时针方向连续跳几个边长。如:若从圈
的顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子朝上的那面上的数字是几,就沿正方形的边按顺时针方向连续跳几个边长。如:若从圈![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落在圈
个边长,落在圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从圈
,就从圈![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落得圈
个边长,落得圈![]() ;…设游戏者从圈
;…设游戏者从圈![]() 起跳.
起跳.
(1)小贤随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(2)小南随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出他与小贤落回到圈
,并指出他与小贤落回到圈![]() 的可能性一样吗?
的可能性一样吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com