
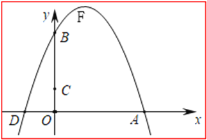
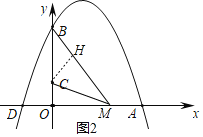
【题目】抛物线![]() 与y轴交于B,与x轴交于点D、A,点A在点D的右边,顶点为F,
与y轴交于B,与x轴交于点D、A,点A在点D的右边,顶点为F,![]()
(1)直接写出点B、A、F的坐标;
(2)设Q在该抛物线上,且![]() ,求点Q的坐标;
,求点Q的坐标;
(3)对大于1常数m,在x轴上是否存在点M,使得![]() ?若存在,求出点M坐标;若不存在,说明理由?
?若存在,求出点M坐标;若不存在,说明理由?
【答案】(1)A(3,0)B(0,3),F(1,4);(2)点Q(2,3)或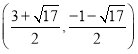 或
或 ;(3)
;(3)![]() 或
或![]()
【解析】
(1)![]() ,令
,令![]() ,解得:
,解得:![]() 或
或![]() ,即可求解;
,即可求解;
(2)连接AB,过点F作直线m平行于直线AB交抛物线与点Q,在BA下方作直线n,使直线m、n与直线AB等距离,过点F作x轴的垂线交AB于点H、交直线n与点![]() ,直线n与抛物线交于点
,直线n与抛物线交于点![]() 、
、![]() ,即可求解;
,即可求解;
(3)由![]() ,则
,则![]() ,
, ,即可求解.
,即可求解.
(1)![]() ,
,
令![]() ,解得:
,解得:![]() 或
或![]() ,
,
令![]() ,则
,则![]() ,故点
,故点![]() ,
,
同理点![]() ;
;
(2)连接AB,过点F作直线m平行于直线AB交抛物线与点Q,在BA下方作直线n,使直线m、n与直线AB等距离,
过点F作x轴的垂线交AB于点H、交直线n与点![]() ,直线n与抛物线交于点
,直线n与抛物线交于点![]() 、
、![]() ,
,

直线BA的表达式为:![]() ,
,
则直线m的表达式为:![]() ,将点F坐标代入上式并解得:
,将点F坐标代入上式并解得:
直线m的表达式为:![]() ,
,
联立![]() 并解得:
并解得:![]() 或
或![]() 舍去
舍去![]() ,
,
故点![]() ;
;
则点![]() ,则
,则![]() ,
,
故直线n的表达式为:![]() ,
,
联立![]() 并解得:
并解得:![]() ,
,
故点Q坐标为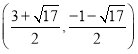 或
或 ,
,
综上,点![]() 或
或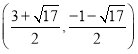 或
或 ;
;
(3)过点C作![]() 于点H,
于点H,
设:![]() ,则
,则![]() ,
,![]() ,
,
![]() ,则
,则![]() ,
,
 ,
,
解得:![]() ,
,
即点![]() 或
或![]() .
.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
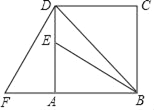
【题目】如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,且点E在线段AD上,若AF=4,∠F=60°.
(1)指出旋转中心和旋转角度;
(2)求DE的长度和∠EBD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
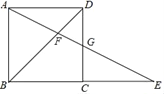
【题目】如图所示,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于E点,对角线BD交AG于F点.已知FG=2,则线段AE的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD为矩形纸片,E、F分别为AB、DC上的点,将此矩形两次翻折,RM和FN为折痕,其中![]() 、
、![]() 分别为A、D的对应点;且点
分别为A、D的对应点;且点![]() 在射线EF上;
在射线EF上;![]() 、
、![]() 分别为B、C的对应点,且点
分别为B、C的对应点,且点![]() 在射线FE上.
在射线FE上.
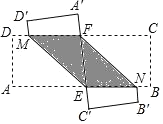
(1)求证:四边形ENFM为平行四边形;
(2)若四边形ENFM为菱形,求∠EMF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中(如图),已知二次函数
中(如图),已知二次函数![]() (其中a、b、c是常数,且a≠0)的图像经过点A(0,-3)、B(1,0)、C(3,0),联结AB、AC.
(其中a、b、c是常数,且a≠0)的图像经过点A(0,-3)、B(1,0)、C(3,0),联结AB、AC.
(1)求这个二次函数的解析式;
(2)点D是线段AC上的一点,联结BD,如果![]() ,求tan∠DBC的值;
,求tan∠DBC的值;
(3)如果点E在该二次函数图像的对称轴上,当AC平分∠BAE时,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了树立文明乡风,推进社会主义新农村建设,某村决定组建村民文体团队,现围绕“你最喜欢的文体活动项目(每人仅限一项)”,在全村范围内随机抽取部村民进行问卷调查,并将调查结果绘制成如下两幅不完整的统计图.请你根据统计图解答下列问题:
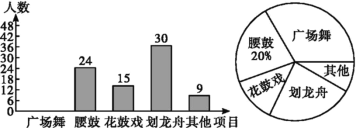
(1)请将条形统计图补充完整;
(2)求扇形统计图中“划龙舟”所在扇形的圆心角的度数;
(3)若在“广场舞、腰鼓、花鼓戏、划龙舟”这四个项目中任选两项组队参加端午节庆典活动,请用列表法或画树状图的方法,求恰好选中“花鼓戏、划龙舟”这两个项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点E为正方形ABCD对角线CA延长线上一点,过E点作EF⊥CB交其延长线于点F,且EF=4,AC=![]()
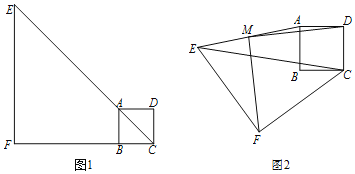
(1)如图1,连接BE,求线段BE的长;
(2)将等腰Rt△CEF绕C点旋转至如图2的位置,连接AE,M点为AE的中点,连接MD、MF,求MD与MF的关系;
(3)将△CEF绕C点旋转一周,请直接写出点M在这个过程中的运动路径长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,以AB为直径画弧分别交BC于点F,交对角线AC于点E,若AB=4,F为BC的中点,则图中阴影部分的面积为 ________;
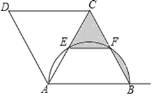
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com