
【题目】为了树立文明乡风,推进社会主义新农村建设,某村决定组建村民文体团队,现围绕“你最喜欢的文体活动项目(每人仅限一项)”,在全村范围内随机抽取部村民进行问卷调查,并将调查结果绘制成如下两幅不完整的统计图.请你根据统计图解答下列问题:
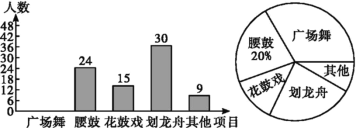
(1)请将条形统计图补充完整;
(2)求扇形统计图中“划龙舟”所在扇形的圆心角的度数;
(3)若在“广场舞、腰鼓、花鼓戏、划龙舟”这四个项目中任选两项组队参加端午节庆典活动,请用列表法或画树状图的方法,求恰好选中“花鼓戏、划龙舟”这两个项目的概率.
【答案】(1)见解析;(2)“划龙舟”所在扇形的圆心角的度数为:90°;(3)两个项目的概率是![]() .
.
【解析】
(1)直接利用腰鼓所占比例以及条形图中人数即可得出这次参与调查的村民人数,利用条形统计图以及样本数量得出喜欢广场舞的人数,补齐条形统计图即可;
(2)利用“划龙舟”人数在样本中所占比例得出“划龙舟”所在扇形的圆心角的度数;
(3)利用树状图法列举出所有的可能进而得出概率.
(1)这次参与调查的村民人数为:24÷20%=120(人),
喜欢广场舞的人数为:120-24-15-30-9=42(人),
如图所示:
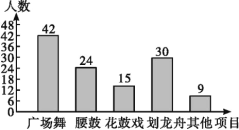
(2)扇形统计图中“划龙舟”所在扇形的圆心角的度数为:
![]() ×360°=90°; ………………
×360°=90°; ………………
(3)如图所示:
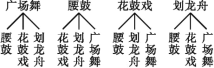
一共有12种可能,恰好选中“花鼓戏、划龙舟”这两个项目的有2种可能,故恰好选中“花鼓戏、划龙舟”这两个项目的概率是![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在边BC,CD上,且BE=CF.连接AE,BF,AE与BF交于点G.下列结论错误的是( )
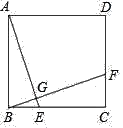
A. AE=BF B. ∠DAE=∠BFC
C. ∠AEB+∠BFC=90° D. AE⊥BF
查看答案和解析>>
科目:初中数学 来源: 题型:
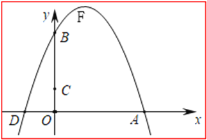
【题目】抛物线![]() 与y轴交于B,与x轴交于点D、A,点A在点D的右边,顶点为F,
与y轴交于B,与x轴交于点D、A,点A在点D的右边,顶点为F,![]()
(1)直接写出点B、A、F的坐标;
(2)设Q在该抛物线上,且![]() ,求点Q的坐标;
,求点Q的坐标;
(3)对大于1常数m,在x轴上是否存在点M,使得![]() ?若存在,求出点M坐标;若不存在,说明理由?
?若存在,求出点M坐标;若不存在,说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省南部的南宫山景区,为吸引游客组团来此旅游特推出了如下门票收费标准:
标准一:如果人数不超过20人,门票价格70元/人
标准二:如果人数超过20人,每超过1人,门票价格降低2元,但门票价格不低于55元/人
(1)若某单位组织22名员工去南宫山景区旅游,则购买门票共需多少元?
(2)若某单位共支付南宫山景区门票费用1500元,试求该单位这次共有多少名员工去南宫山旅游.
查看答案和解析>>
科目:初中数学 来源: 题型:
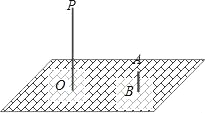
【题目】如图,晚上,小亮在广场上乘凉.图中线段AB表示站在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯.
(1)请你在图中画出小亮在照明灯(P)照射下的影子;
(2)如果灯杆高PO=12m,小亮的身高AB=1.6m,小亮与灯杆的距离BO=13m,请求出小亮影子的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt![]() 中,∠A=90°,AC=4,
中,∠A=90°,AC=4,![]() ,将
,将![]() 沿着斜边BC翻折,点A落在点
沿着斜边BC翻折,点A落在点![]() 处,点D、E分别为边AC、BC的中点,联结DE并延长交
处,点D、E分别为边AC、BC的中点,联结DE并延长交![]() 所在直线于点F,联结
所在直线于点F,联结![]() ,如果
,如果![]() 为直角三角形时,那么
为直角三角形时,那么![]() ____________
____________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com