
【题目】在平面直角坐标系![]() 中(如图),已知二次函数
中(如图),已知二次函数![]() (其中a、b、c是常数,且a≠0)的图像经过点A(0,-3)、B(1,0)、C(3,0),联结AB、AC.
(其中a、b、c是常数,且a≠0)的图像经过点A(0,-3)、B(1,0)、C(3,0),联结AB、AC.
(1)求这个二次函数的解析式;
(2)点D是线段AC上的一点,联结BD,如果![]() ,求tan∠DBC的值;
,求tan∠DBC的值;
(3)如果点E在该二次函数图像的对称轴上,当AC平分∠BAE时,求点E的坐标.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)E(2,
;(3)E(2,![]() )
)
【解析】
(1)直接利用待定系数法,把A、B、C三点代入解析式,即可得到答案;
(2)过点D作DH⊥BC于H,在△ABC中,设AC边上的高为h,利用面积的比得到![]() ,然后求出DH和BH,即可得到答案;
,然后求出DH和BH,即可得到答案;
(3)延长AE至x轴,与x轴交于点F,先证明△OAB∽△OFA,求出点F的坐标,然后求出直线AF的方程,即可求出点E的坐标.
解:(1)将A(0,-3)、B(1,0)、C(3,0)代入![]() 得,
得,
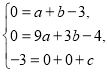
解得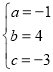 ,
,
∴此抛物线的表达式是:![]() .
.
(2)过点D作DH⊥BC于H,

在△ABC中,设AC边上的高为h,则![]() ,
,
又∵DH//y轴,
∴![]() .
.
∵OA=OC=3,则∠ACO=45°,
∴△CDH为等腰直角三角形,
∴![]() .
.
∴![]() .
.
∴tan∠DBC=![]() .
.
(3)延长AE至x轴,与x轴交于点F,

∵OA=OC=3,
∴∠OAC=∠OCA=45°,
∵∠OAB=∠OAC![]() ∠BAC=45°
∠BAC=45°![]() ∠BAC,∠OFA=∠OCA
∠BAC,∠OFA=∠OCA![]() ∠FAC=45°
∠FAC=45°![]() ∠FAC,
∠FAC,
∵∠BAC=∠FAC,
∴∠OAB=∠OFA.
∴△OAB∽△OFA,
∴![]() .
.
∴OF=9,即F(9,0);
设直线AF的解析式为y=kx+b(k≠0),
可得![]() ,解得
,解得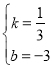 ,
,
∴直线AF的解析式为:![]() ,
,
将x=2代入直线AF的解析式得:![]() ,
,
∴E(2,![]() ).
).


科目:初中数学 来源: 题型:
【题目】把函数![]() 的图象绕点
的图象绕点![]() 旋转
旋转![]() ,得到新函数
,得到新函数![]() 的图象,我们称
的图象,我们称![]() 是
是![]() 关于点
关于点![]() 的相关函数.
的相关函数.![]() 的图象的对称轴与
的图象的对称轴与![]() 轴交点坐标为
轴交点坐标为![]() .
.
(1)填空:![]() 的值为 (用含
的值为 (用含![]() 的代数式表示)
的代数式表示)
(2)若![]() ,当
,当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,且
,且![]() ,求
,求![]() 的解析式;
的解析式;
(3)当![]() 时,
时,![]() 的图象与
的图象与![]() 轴相交于
轴相交于![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧).与
的右侧).与![]() 轴相交于点
轴相交于点![]() .把线段
.把线段![]() 原点
原点![]() 逆时针旋转
逆时针旋转![]() ,得到它的对应线段
,得到它的对应线段![]() ,若线
,若线![]() 与
与![]() 的图象有公共点,结合函数图象,求
的图象有公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料![]() ,乙种原料
,乙种原料![]() ,现用两种原料生产处
,现用两种原料生产处![]() 两种产品共
两种产品共![]() 件,已知生产每件
件,已知生产每件![]() 产品需甲种原料
产品需甲种原料![]() ,乙种原料
,乙种原料![]() ,且每件
,且每件![]() 产品可获得
产品可获得![]() 元;生产每件
元;生产每件![]() 产品甲种原料
产品甲种原料![]() ,乙种原料
,乙种原料![]() ,且每件
,且每件![]() 产品可获利润
产品可获利润![]() 元,设生产
元,设生产![]() 产品
产品![]() 件(产品件数为整数件),根据以上信息解答下列问题:
件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产![]() 两种产品的方案有哪几种?
两种产品的方案有哪几种?
(2)设生产这![]() 件产品可获利
件产品可获利![]() 元,写出关于
元,写出关于![]() 的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
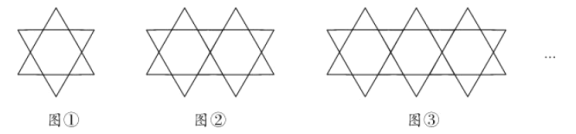
【题目】将大小相同的正三角形按如图所示的规律拼图案,其中第①个图案中有6个小三角形和1个正六边形;第②个图案中有10个小三角形和2个正六边形;第③个图案中有14个小三角形和3个正六边形;…;按此规律排列下去,已知一个正六边形的面积为![]() ,一个小三角形的面积为
,一个小三角形的面积为![]() ,则第③个图案中所有的小三角形和正六边形的面积之和为______.(结果用含
,则第③个图案中所有的小三角形和正六边形的面积之和为______.(结果用含![]() 、
、![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)如图①,点C是AB中点,CD⊥AB,P是CD上任意一点,由三角形全等的判定方法“SAS”易证△PAC≌△PBC,得到线段垂直平分线的一条性质“线段垂直平分线上的点到线段两端的距离相等”

(探究)如图②,在平面直角坐标系中,直线y=-![]() x+1分别交x轴、y轴于点A和点B,点C是AB中点,CD⊥AB交OA于点D,连结BD,求BD的长
x+1分别交x轴、y轴于点A和点B,点C是AB中点,CD⊥AB交OA于点D,连结BD,求BD的长
(应用)如图③
(1)将线段AB绕点A顺时针旋转90°得到线段AB′,请在图③网格中画出线段AB;
(2)若存在一点P,使得PA=PB′,且∠APB′≠90°,当点P的横、纵坐标均为整数时,则AP长度的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“大美湿地,水韵盐城”.某校数学兴趣小组就“最想去的盐城市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:

请根据图中提供的信息,解答下列问题:
(1)求被调查的学生总人数;
(2)补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)若该校共有800名学生,请估计“最想去景点B“的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解放桥是天津市的标志性建筑之一,是一座全钢结构的部分可开启的桥梁,
(I)如图①,已知解放桥可开启部分的桥面的跨度AB等于47m,从AB的中点C处开启,则AC开启至A'C'的位置时,A'C'的长为 .
(II)如图②,某校数学兴趣小组要测量解放桥的全长PQ,在观景平台M处测得∠PMQ=54°,沿河岸MQ前行,在观景平台N处测得∠PNQ=73°。已知PQ⊥MQ,MN=40m,求解放桥的全长PQ(tan54°≈1.4,tan73°≈3.3,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年4月22日是第50个世界地球日,某校在八年级5个班中,每班各选拔10名学生参加“环保知识竞赛”并评出了一、二、三等奖各若干名,学校将获奖情况绘成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:
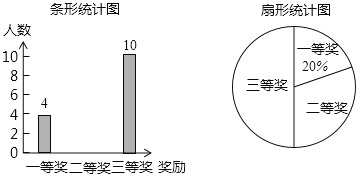
(1)求本次竞赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)已知甲、乙、丙、丁4位同学获得一等奖,学校将采取随机抽签的方式在4人中选派2人参加上级团委组织的“爱护环境、保护地球”知识竞赛,请求出抽到的2人恰好是甲和乙的概率(用画树状图或列表等方法求解).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com