
【题目】我们知道:任何有理数的平方都是一个非负数,即对于任何有理数a,都有![]() 成立,所以,当
成立,所以,当![]() 时,
时,![]() 有最小值0.
有最小值0.
(应用):(1)代数式![]() 有最小值时,
有最小值时,![]() ;
;
(2)代数式![]() 的最小值是 ;
的最小值是 ;
(探究):求代数式![]() 的最小值,小明是这样做的:
的最小值,小明是这样做的:
![]()
![]()
![]()
∴当![]() 时,代数式
时,代数式![]() 有最小值,最小值为5.
有最小值,最小值为5.
(3)请你参照小明的方法,求代数式![]() 的最小值,并求此时a的值.
的最小值,并求此时a的值.
(拓展):(4)若![]() ,直接写出y的取值范围.
,直接写出y的取值范围.
【答案】(1)1;(2)3;(3)-12;(4)![]()
【解析】
(1)由(x-1)2≥0可得x=1时,取得最小值0;
(2)由m2≥0知m2+3≥3可得答案;
(3)将原式![]() 变形为(a-3)2-12,参照小明的方法求解即可;
变形为(a-3)2-12,参照小明的方法求解即可;
(4)由y=-4t2+12t+6=-4(t-![]() )2+15知-4(t-
)2+15知-4(t-![]() )2+15≤15,从而得出答案.
)2+15≤15,从而得出答案.
(1)![]() ,当
,当![]() 时,可得最小值为0,
时,可得最小值为0,
故答案为:1;
(2)![]() ,
,
![]() 的最小值是当
的最小值是当![]() 时,最小值为3,
时,最小值为3,
故答案为:3;
(3)![]()
![]() 当
当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;
;
(4)y=-4t2+12t+6
=-4(t2-3t)+6
=-4(t2-3t+![]() -
-![]() )+6
)+6
=-4(t-![]() )2+15,
)2+15,
∵(t-![]() )2≥0,
)2≥0,
∴-4(t-![]() )2≤0,
)2≤0,
则-4(t-![]() )2+15≤15,即y≤15.
)2+15≤15,即y≤15.


科目:初中数学 来源: 题型:
【题目】如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的
俯角为α其中tanα=2![]() ,无人机的飞行高度AH为500
,无人机的飞行高度AH为500![]() 米,桥的长度为1255米.
米,桥的长度为1255米.
①求点H到桥左端点P的距离;
②若无人机前端点B测得正前方的桥的右端点Q的俯角为30°,求这架无人机的长度AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程:x2﹣5x﹣6=0
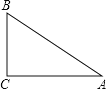
(2)如图,△ABC中∠C=90°
①将△ABC绕A点逆时针旋转90°,画出旋转后的三角形△AB′C′;
②若BC=3,AC=4,B点旋转后的对应是B′,求![]() 的长
的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),某数学活动小组经探究发现:在⊙O中,直径AB与弦CD相交于点P,此时PA· PB=PC·PD
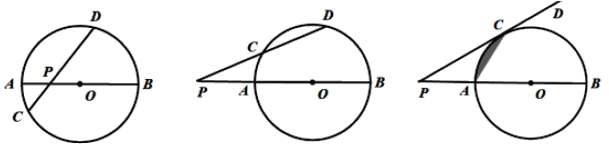
(1)如图(2),若AB与CD相交于圆外一点P, 上面的结论是否成立?请说明理由.
(2)如图(3),将PD绕点P逆时针旋转至与⊙O相切于点C, 直接写出PA、PB、PC之间的数量关系.
(3)如图(3),直接利用(2)的结论,求当 PC= ![]() ,PA=1时,阴影部分的面积.
,PA=1时,阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD为矩形纸片,E、F分别为AB、DC上的点,将此矩形两次翻折,RM和FN为折痕,其中![]() 、
、![]() 分别为A、D的对应点;且点
分别为A、D的对应点;且点![]() 在射线EF上;
在射线EF上;![]() 、
、![]() 分别为B、C的对应点,且点
分别为B、C的对应点,且点![]() 在射线FE上.
在射线FE上.
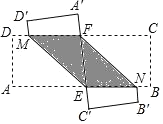
(1)求证:四边形ENFM为平行四边形;
(2)若四边形ENFM为菱形,求∠EMF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象交于A(1,a)、B两点.
)的图象交于A(1,a)、B两点.
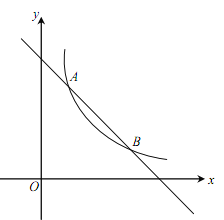
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中(如图),已知二次函数
中(如图),已知二次函数![]() (其中a、b、c是常数,且a≠0)的图像经过点A(0,-3)、B(1,0)、C(3,0),联结AB、AC.
(其中a、b、c是常数,且a≠0)的图像经过点A(0,-3)、B(1,0)、C(3,0),联结AB、AC.
(1)求这个二次函数的解析式;
(2)点D是线段AC上的一点,联结BD,如果![]() ,求tan∠DBC的值;
,求tan∠DBC的值;
(3)如果点E在该二次函数图像的对称轴上,当AC平分∠BAE时,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A1、A2、A3、…、An在x轴上,且OA1=A1A2=A2A3=…=An﹣1An=1,分别过点A1、A2、A3、……、An作x轴的垂线,交反比例函数y=![]() (x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2019=_____.
(x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2019=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一块锐角三角形余料,边BC=120 mm,高AD=80mm,要把它加工成矩形零件PQMN,使矩形PQMN的边QM在BC上,其余两个项点P,N分别在AB,AC上.
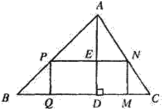
(1)当矩形的边PN=PQ时,求此时矩形零件PQMN的面积;
(2)求这个矩形零件PQMN面积S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com