
【题目】如图,已知点A1、A2、A3、…、An在x轴上,且OA1=A1A2=A2A3=…=An﹣1An=1,分别过点A1、A2、A3、……、An作x轴的垂线,交反比例函数y=![]() (x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2019=_____.
(x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2019=_____.

科目:初中数学 来源: 题型:
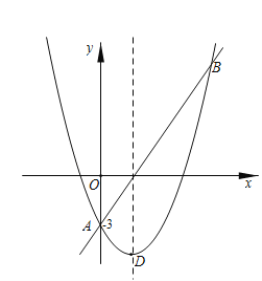
【题目】如图,直线AB和抛物线的交点是A(0,﹣3),B(5,9),已知抛物线的顶点D的横坐标是2.
(1)求抛物线的解析式及顶点坐标;
(2)在x轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不在,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:任何有理数的平方都是一个非负数,即对于任何有理数a,都有![]() 成立,所以,当
成立,所以,当![]() 时,
时,![]() 有最小值0.
有最小值0.
(应用):(1)代数式![]() 有最小值时,
有最小值时,![]() ;
;
(2)代数式![]() 的最小值是 ;
的最小值是 ;
(探究):求代数式![]() 的最小值,小明是这样做的:
的最小值,小明是这样做的:
![]()
![]()
![]()
∴当![]() 时,代数式
时,代数式![]() 有最小值,最小值为5.
有最小值,最小值为5.
(3)请你参照小明的方法,求代数式![]() 的最小值,并求此时a的值.
的最小值,并求此时a的值.
(拓展):(4)若![]() ,直接写出y的取值范围.
,直接写出y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,抛物线![]() 经过点A(-2,0),B(4,0)两点,与
经过点A(-2,0),B(4,0)两点,与![]() 轴交于点C,点D是抛物线上一个动点,设点D的横坐标为
轴交于点C,点D是抛物线上一个动点,设点D的横坐标为![]() .连接AC,BC,DB,DC,
.连接AC,BC,DB,DC,
(1)求抛物线的函数表达式;
(2)△BCD的面积等于△AOC的面积的![]() 时,求
时,求![]() 的值;
的值;
(3)在(2)的条件下,若点M是![]() 轴上的一个动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
轴上的一个动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省南部的南宫山景区,为吸引游客组团来此旅游特推出了如下门票收费标准:
标准一:如果人数不超过20人,门票价格70元/人
标准二:如果人数超过20人,每超过1人,门票价格降低2元,但门票价格不低于55元/人
(1)若某单位组织22名员工去南宫山景区旅游,则购买门票共需多少元?
(2)若某单位共支付南宫山景区门票费用1500元,试求该单位这次共有多少名员工去南宫山旅游.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当今,越来越多的青少年在观看影片《流浪地球》后,更加喜欢同名科幻小说,该小说销量也急剧上升.书店为满足广大顾客需求,订购该科幻小说若干本,每本进价为20元.根据以往经验:当销售单价是25元时,每天的销售量是250本;销售单价每上涨1元,每天的销售量就减少10本,书店要求每本书的利润不低于10元且不高于18元.
(1)直接写出书店销售该科幻小说时每天的销售量![]() (本)与销售单价
(本)与销售单价![]() (元)之间的函数关系式及自变量的取值范围.
(元)之间的函数关系式及自变量的取值范围.
(2)书店决定每销售1本该科幻小说,就捐赠![]() 元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求
元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(t,0),B(t+2,0).对于线段AB和点P给出如下定义:当∠APB=90°时,称点P为线段AB的“直角点”.
(Ⅰ)当t=﹣1时,点C(0,1),判断点C是否为线段AB的“直角点”,并说明理由;
(Ⅱ)已知抛物线y=ax2+bx(a>0,b<0)的顶点为M,与x轴交于A(t,0),B(t+2,0),若点M为线段AB的“直角点”,求出此抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,连接
的中点,连接![]() .
.

(1)在图①中,![]() 的值为______;
的值为______;![]() 的值为______.
的值为______.
(2)若将![]() 绕点
绕点![]() 逆时针方向旋转得到
逆时针方向旋转得到![]() ,点
,点![]() 、
、![]() 的对应点为
的对应点为![]() 、
、![]() ,在旋转过程中
,在旋转过程中![]() 的大小是否发生变化?请仅就图②的情形给出证明.
的大小是否发生变化?请仅就图②的情形给出证明.
(3)当![]() 在旋转一周的过程中,
在旋转一周的过程中,![]() ,
,![]() ,
,![]() 三点共线时,请你直接写出线段
三点共线时,请你直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中,∠C=90°,点O在AC上,以AO为半径的⊙O交AB于D, BD的垂直平分线交BD于F,交BC于E,连接DE.

(1)求证:DE是⊙O的切线;
(2)若∠B=30°,BC=![]() ,且AD∶DF=1∶2,求⊙O的直径.
,且AD∶DF=1∶2,求⊙O的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com