
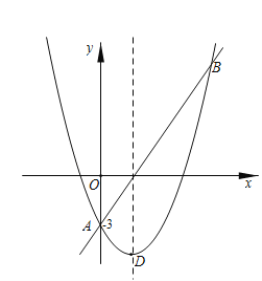
【题目】如图,直线AB和抛物线的交点是A(0,﹣3),B(5,9),已知抛物线的顶点D的横坐标是2.
(1)求抛物线的解析式及顶点坐标;
(2)在x轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不在,请说明理由;
【答案】(1)抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣3,顶点D的坐标为(2,﹣
x﹣3,顶点D的坐标为(2,﹣![]() );
);
(2)存在,C坐标为:(4![]() ,0)或(﹣4
,0)或(﹣4![]() ,0),(5+
,0),(5+![]() ,0)或(5﹣2
,0)或(5﹣2![]() ,0),(
,0),(![]() ,0),
,0),
【解析】
(1)根据抛物线的顶点D的横坐标为2,可设抛物线的解析式为![]() ,再将点A和B的坐标代入即可得;
,再将点A和B的坐标代入即可得;
(2)先求出AB的长,然后分哪两条边为等腰![]() 的腰,设点C的坐标为
的腰,设点C的坐标为![]() ,根据两腰相等,利用两点之间距离公式建立等式,求解即可.
,根据两腰相等,利用两点之间距离公式建立等式,求解即可.
(1)抛物线的顶点D的横坐标为2,可设抛物线的解析式为:![]()
将![]() 代入得
代入得![]()
解得: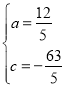
则抛物线的解析式为:![]() (或写成一般形式
(或写成一般形式![]() )
)
由顶点式可得顶点D的坐标为![]() ;
;
( 2)设点C坐标![]()
因![]()
则![]()
![]()
![]()
①当![]() 时,则
时,则![]()
解得:![]() ,即点C坐标为:
,即点C坐标为:![]() 或
或![]()
②当![]() 时,则
时,则![]()
解得:![]() ,即点C坐标为
,即点C坐标为![]() 或
或![]()
③当![]() 时,则
时,则![]()
解得:![]() ,即点C坐标为
,即点C坐标为![]()
综上,存在这样的点C,点C的坐标为![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() .
.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
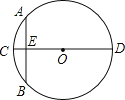
【题目】“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,求直径CD的长”.(1尺=10寸)则CD=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的
俯角为α其中tanα=2![]() ,无人机的飞行高度AH为500
,无人机的飞行高度AH为500![]() 米,桥的长度为1255米.
米,桥的长度为1255米.
①求点H到桥左端点P的距离;
②若无人机前端点B测得正前方的桥的右端点Q的俯角为30°,求这架无人机的长度AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是![]() (
(![]() ,称为黄金比例),如图,著名的“断臂维纳斯”便是如此,此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是
,称为黄金比例),如图,著名的“断臂维纳斯”便是如此,此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是![]() ,若某人的身材满足上述两个黄金比例,且头顶至咽喉的长度为
,若某人的身材满足上述两个黄金比例,且头顶至咽喉的长度为![]() ,则其升高可能是( )
,则其升高可能是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
| … | -2 | -1 | 0 | 1 | 2 | … |
| … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中正确的是______.(填写序号)
①抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ; ②函数
; ②函数![]() 的最大值为6;
的最大值为6;
③抛物线的对称轴是直线![]() ; ④在对称轴左侧,
; ④在对称轴左侧,![]() 随
随![]() 增大而增大.
增大而增大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程:x2﹣5x﹣6=0
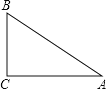
(2)如图,△ABC中∠C=90°
①将△ABC绕A点逆时针旋转90°,画出旋转后的三角形△AB′C′;
②若BC=3,AC=4,B点旋转后的对应是B′,求![]() 的长
的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),某数学活动小组经探究发现:在⊙O中,直径AB与弦CD相交于点P,此时PA· PB=PC·PD
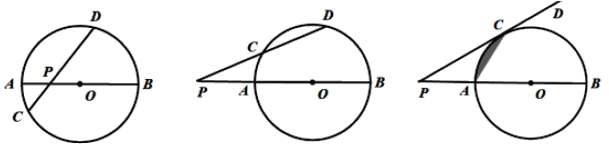
(1)如图(2),若AB与CD相交于圆外一点P, 上面的结论是否成立?请说明理由.
(2)如图(3),将PD绕点P逆时针旋转至与⊙O相切于点C, 直接写出PA、PB、PC之间的数量关系.
(3)如图(3),直接利用(2)的结论,求当 PC= ![]() ,PA=1时,阴影部分的面积.
,PA=1时,阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A1、A2、A3、…、An在x轴上,且OA1=A1A2=A2A3=…=An﹣1An=1,分别过点A1、A2、A3、……、An作x轴的垂线,交反比例函数y=![]() (x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2019=_____.
(x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2019=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com