
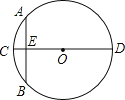
【题目】“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,求直径CD的长”.(1尺=10寸)则CD=_____.
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
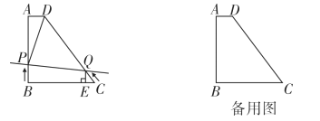
【题目】如图,已知四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求四边形![]() 的面积
的面积![]() ;
;
(2)动点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度,沿
出发,以每秒1个单位长度的速度,沿![]() 方向,向点
方向,向点![]() 运动;动点
运动;动点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度,沿
出发,以每秒1个单位长度的速度,沿![]() 方向,向点
方向,向点![]() 运动,过点
运动,过点![]() 作
作![]() 于点
于点![]() .若
.若![]() 、
、![]() 两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为
两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为![]() .问:
.问:
①当点![]() 在
在![]() 上运动时,是否存在这样的
上运动时,是否存在这样的![]() ,使得直线
,使得直线![]() 将四边形
将四边形![]() 的周长平分?若存在,请求出
的周长平分?若存在,请求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
②在运动过程中,是否存在这样的![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出所有符合条件的
相似?若存在,请求出所有符合条件的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
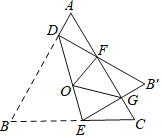
【题目】如图,等边三角形ABC边长是定值,点O是它的外心,过点O任意作一条直线分别交AB,BC于点D,E.将△BDE沿直线DE折叠,得到△B′DE,若B′D,B′E分别交AC于点F,G,连接OF,OG,则下列判断错误的是( )
A. △ADF≌△CGE
B. △B′FG的周长是一个定值
C. 四边形FOEC的面积是一个定值
D. 四边形OGB'F的面积是一个定值
查看答案和解析>>
科目:初中数学 来源: 题型:
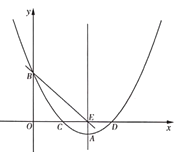
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,过抛物线的顶点
,过抛物线的顶点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足为点
,垂足为点![]() ,作直线
,作直线![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 为第一象限内直线
为第一象限内直线![]() 上的一点,连接
上的一点,连接![]() ,取
,取![]() 的中点
的中点![]() ,作射线
,作射线![]() 交抛物线于点
交抛物线于点![]() ,设线段
,设线段![]() 的长为
的长为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 之间的函数关系式(不要求写出自变量
之间的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,在线段![]() 上有一点
上有一点![]() ,连接
,连接![]() ,
,![]() ,线段
,线段![]() 交线段
交线段![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经中共中央决定设立河北雄安新区,这一重大措施必将带动首都及周边区域向更高水平发展,同时也会带来更多商机.某水果经销商在第一周购进一批水果1160件,预计在第二周进行试销,购进价格为每件10元,若售价为每件12元,则可全部售出;若售价每涨价0.1元,销量就减少2件.
(1)若该经销商在第二周的销量不低于1100件,则售价应不高于多少元?
(2)由于销量较好,第三周水果进价比第一周每件增加了20%,该经销商增加了进货量,并加强了宣传力度,结果第三周的销量比第二周在(1)条件下的最低销量增加了m%,但售价比第二周在(1)条件下的最高售价减少了![]() m%,结果第三周利润达到3388元,求m的值(m>10).
m%,结果第三周利润达到3388元,求m的值(m>10).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个转盘.转盘分成8个相同的图形,颜色分为红、绿、黄三种.指针的位置固定,转动转盘后任其兹有停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个图形的交线时,当作指向右边的图形).求下列事件的概率:
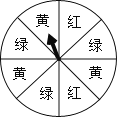
(1)指针指向红色;
(2)指针指向黄色或绿色。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+m图象过点A(1,0),交y轴于点![]() ,
,![]() 为y轴负半轴上一点,且
为y轴负半轴上一点,且![]() ,过
,过![]() 、
、![]() 两点的抛物线交直线
两点的抛物线交直线![]() 于点
于点![]() ,且CD//x轴.
,且CD//x轴.
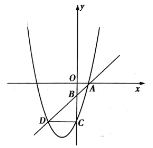
(1)求这条抛物线的解析式;
(2)观察图象,写出使一次函数值小于二次函数值时![]() 的取值范围;
的取值范围;
(3)在题中的抛物线上是否存在一点![]() ,使得
,使得![]() 为直角?若存在,求出点
为直角?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,﹣3),B(5,9),已知抛物线的顶点D的横坐标是2.
(1)求抛物线的解析式及顶点坐标;
(2)在x轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不在,请说明理由;
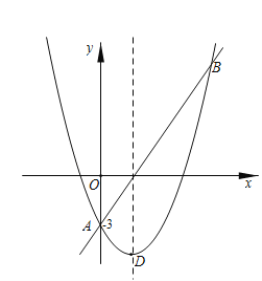
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com