
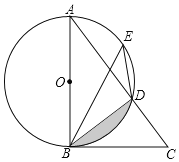
【题目】 如图,AB是⊙O的直径,点E是AD上的一点,∠DBC=∠BED
(1)求证:BC是⊙O的切线;
(2)已知AD=3,CD=1,求图中阴影部分的面积.
【答案】(1)证明见解析;(2)![]() ﹣
﹣![]() .
.
【解析】
(1)根据圆周角定理得∠BAD=∠BED,加上∠DBC=∠BED,所以∠BAD=∠DBC,再由AB为直径得∠ADB=90°,所以∠BAD+∠ABD=90°,于是得到∠DBC+∠ABD=90°,即∠CBO=90°,然后根据切线的判断定理可判断BC为⊙O的切线;
(2)求出BD=![]() ,连结OD,作DH⊥AB于H,根据勾股定理计算出AB=2
,连结OD,作DH⊥AB于H,根据勾股定理计算出AB=2![]() ,则OB=OD=
,则OB=OD=![]() ,于是可判断△OBD为等边三角形,则∠BOD=60°,根据面积公式求出DH=
,于是可判断△OBD为等边三角形,则∠BOD=60°,根据面积公式求出DH=![]() ,然后根据扇形面积公式和三角形面积公式,利用阴影部分的面积=S扇形OBD-S△OBD进行计算即可.
,然后根据扇形面积公式和三角形面积公式,利用阴影部分的面积=S扇形OBD-S△OBD进行计算即可.
解:(1)∵∠BAD=∠BED,
而∠DBC=∠BED,
∴∠BAD=∠DBC,
∵AB为直径,
∴∠ADB=90°,
∴∠BAD+∠ABD=90°
∴∠DBC+∠ABD=90°,即∠CBO=90°,
∴AB⊥BC,
∴BC为⊙O的切线;
(2)连结OD,作DH⊥AB于H,
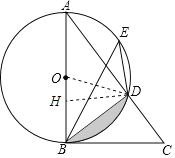
∵∠ABC=90°,BD⊥AC,
根据(1)知∠BAD=∠DBC
∴△ABD∽△BDC
∴BD2=ADCD=3×1=3,
∴BD=![]() ,
,
∴AB=![]() =
=![]() =2
=2![]() ,
,
∴OB=OD=![]() ,
,
∴OB=OD=BD,
∴△OBD为等边三角形,
∴∠BOD=60°,
∵![]() ABDH=
ABDH=![]() ADBD,
ADBD,
∴DH=![]() =
=![]() =
=![]() ,
,
∴S阴影=S扇形OBD﹣S△OBD=![]() ﹣
﹣![]() ×
×![]() ×
×![]() =
=![]() ﹣
﹣![]() .
.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=ax2+bx+c的图象如图所示,那么关于x的一元二次方程ax2+bx+c-3=0的根的情况是( )
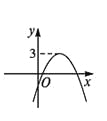
A. 有两个不相等的实数根
B. 有两个异号的实数根
C. 有两个相等的实数根
D. 没有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,![]() 是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF,下列说法不正确的是
是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF,下列说法不正确的是![]()
![]()

A. 四边形CEDF是平行四边形
B. 当![]() 时,四边形CEDF是矩形
时,四边形CEDF是矩形
C. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
D. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
已知二次函数y=﹣![]() x2+
x2+![]() x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)求证:△ABC为直角三角形;
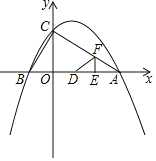
(3)如图,动点E,F同时从点A出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒![]() 个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
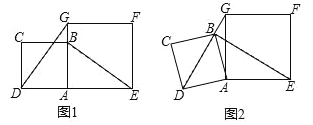
【题目】正方形ABCD和正方形AEFG的边长分别为2和![]() ,点B在边AG上,点D在线段EA的延长线上,连接BE.
,点B在边AG上,点D在线段EA的延长线上,连接BE.
(1)如图1,求证:DG⊥BE;
(2)如图2,将正方形ABCD绕点A按逆时针方向旋转,当点B恰好落在线段DG上时,求线段BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com