
°æƒø°ø‘⁄“ª¥Œ ˝—ߪÓ∂ØøŒ…œ£¨¿œ ¶»√Õ¨—ß√«µΩ≤Ÿ≥°…œ≤‚¡ø∆Ï∏Àµƒ∏þ∂»£¨»ª∫Ûªÿ¿¥Ωª¡˜∏˜◊‘µƒ≤‚¡ø∑Ω∑®£Æ–°∑ºµƒ≤‚¡ø∑Ω∑® «£∫ƒ√“ª∏˘∏þ3.5√◊µƒ÷Ò∏Õ÷±¡¢‘⁄¿Î∆Ï∏À27√◊µƒC¥¶£®»ÁÕº£©£¨»ª∫Û—ÿBC∑ΩœÚ◊þµΩD¥¶£¨’‚ ±ƒø≤‚∆Ï∏À∂•≤øA”Î÷Ò∏Õ∂•≤øE«°∫√‘⁄Õ¨“ª÷±œþ…œ£¨”÷≤‚µ√C°¢D¡Ωµ„µƒæý¿ÎŒ™3√◊£¨–°∑ºµƒƒø∏þŒ™1.5√◊£¨’‚—˘±„ø…÷™µ¿∆Ï∏Àµƒ∏þ£Æƒ„»œŒ™’‚÷÷≤‚¡ø∑Ω∑® «∑Òø…––£ø«ÎÀµ√˜¿Ì”…£Æ

°æ¥∞∏°ø’‚÷÷≤‚¡ø∑Ω∑®ø…––£¨∆Ï∏Àµƒ∏þŒ™21.5√◊£Æ
°æΩ‚Œˆ°ø
∏˘æð“—÷™µ√≥ˆπ˝F◊˜FG°ÕAB”⁄G£¨ΩªCE”⁄H£¨¿˚”√œýÀ∆»˝Ω«–Œµƒ≈–∂®µ√≥ˆ°˜AGF°◊°˜EHF£¨‘Ÿ¿˚”√œýÀ∆»˝Ω«–Œµƒ–‘÷ µ√≥ˆº¥ø…£Æ
’‚÷÷≤‚¡ø∑Ω∑®ø…––£Æ
¿Ì”…»Áœ¬£∫
…Ë∆Ï∏À∏þAB=x£Æπ˝F◊˜FG°ÕAB”⁄G£¨ΩªCE”⁄H£®»ÁÕº£©£Æ
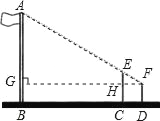
À˘“‘°˜AGF°◊°˜EHF£Æ
“ÚŒ™FD=1.5£¨GF=27+3=30£¨HF=3£¨
À˘“‘EH=3.5©Å1.5=2£¨AG=x©Å1.5£Æ
”…°˜AGF°◊°˜EHF£¨
µ√![]() £¨
£¨
º¥![]() £¨
£¨
À˘“‘x©Å1.5=20£¨
Ω‚µ√x=21.5£®√◊£©
¥£∫∆Ï∏Àµƒ∏þŒ™21.5√◊£Æ


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™‘⁄ ˝÷·…œ”–![]() ¡Ωµ„£¨µ„
¡Ωµ„£¨µ„![]() ±Ì 浃 ˝Œ™
±Ì 浃 ˝Œ™![]() £¨µ„
£¨µ„![]() ‘⁄
‘⁄![]() µ„µƒ◊Û±þ£¨«“
µ„µƒ◊Û±þ£¨«“![]() £Æ»Ù”–“ª∂ص„
£Æ»Ù”–“ª∂ص„![]() ¥” ˝÷·…œµ„
¥” ˝÷·…œµ„![]() ≥ˆ∑¢£¨“‘√ø√Î
≥ˆ∑¢£¨“‘√ø√Î![]() ∏ˆµ•Œª≥§∂»µƒÀŸ∂»—ÿ ˝÷·œÚ◊Û‘»ÀŸ‘À∂Ø£¨∂ص„
∏ˆµ•Œª≥§∂»µƒÀŸ∂»—ÿ ˝÷·œÚ◊Û‘»ÀŸ‘À∂Ø£¨∂ص„![]() ¥”µ„
¥”µ„![]() ≥ˆ∑¢£¨“‘√ø√Î
≥ˆ∑¢£¨“‘√ø√Î![]() ∏ˆµ• Œª≥§∂»µƒÀŸ∂»—ÿ◊≈ ˝÷·œÚ”“‘»ÀŸ‘À∂Ø£¨…Ë‘À∂Ø ±º‰Œ™
∏ˆµ• Œª≥§∂»µƒÀŸ∂»—ÿ◊≈ ˝÷·œÚ”“‘»ÀŸ‘À∂Ø£¨…Ë‘À∂Ø ±º‰Œ™![]() √Σ¨Ω‚戓‘œ¬Œ £∫
√Σ¨Ω‚戓‘œ¬Œ £∫
![]() –¥≥ˆ ˝÷·…œµ„
–¥≥ˆ ˝÷·…œµ„![]() À˘±Ì 浃 ˝£ª
À˘±Ì 浃 ˝£ª
![]() »Ùµ„
»Ùµ„![]() ∑÷±¥”
∑÷±¥”![]() ¡Ωµ„Õ¨ ±≥ˆ∑¢£¨Œ µ„
¡Ωµ„Õ¨ ±≥ˆ∑¢£¨Œ µ„![]() ‘À∂Ø∂ý…Ÿ√Δε„
‘À∂Ø∂ý…Ÿ√Δε„![]() œýæý
œýæý![]() ∏ˆµ•Œª≥§∂»£ø
∏ˆµ•Œª≥§∂»£ø
![]() ÃΩÀ˜Œ £∫»Ù
ÃΩÀ˜Œ £∫»Ù![]() Œ™
Œ™![]() µƒ÷–µ„£¨
µƒ÷–µ„£¨![]() Œ™
Œ™![]() µƒ÷–µ„£¨µ±µ„
µƒ÷–µ„£¨µ±µ„![]() ‘⁄œþ∂Œ
‘⁄œþ∂Œ![]() …œ‘À∂Øπ˝≥Ã÷–£¨ÃΩÀ˜œþ∂Œ
…œ‘À∂Øπ˝≥Ã÷–£¨ÃΩÀ˜œþ∂Œ![]() ”Îœþ∂Œ
”Îœþ∂Œ![]() µƒ ˝¡øπÿœµ£®–¥≥ˆπ˝≥ã©£Æ
µƒ ˝¡øπÿœµ£®–¥≥ˆπ˝≥ã©£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øœ¬±Ì «ƒ≥–£°∞∫”ƒœ °∫∫◊”Ã˝–¥¥Û»¸≥ı»¸°±π⁄æ¸◊È≥…‘±µƒƒÍ¡‰∑÷≤º
ƒÍ¡‰/ÀÍ | 12 | 13 | 14 | 15 |
»À ˝ | 5 | 15 | x | 12©Åx |
∂‘”⁄≤ªÕ¨µƒx£¨œ¬¡–πÿ”⁄ƒÍ¡‰µƒÕ≥º∆¡ø≤ªª·∑¢…˙∏ƒ±‰µƒ «£®°°°°£©
A. ∆Ωæ˘ ˝°¢÷–Œª ˝ B. ∆Ωæ˘ ˝°¢∑Ω≤Ó C. ÷⁄ ˝°¢÷–Œª ˝ D. ÷–Œª ˝°¢∑Ω≤Ó
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™AB «°—Oµƒ÷±æ∂£¨œ“CD°ÕAB”⁄H£¨π˝CD—”≥§œþ…œ“ªµ„E◊˜°—Oµƒ«–œþΩªABµƒ—”≥§œþ”⁄F£¨«–µ„Œ™G£¨¡¨Ω”AGΩªCD”⁄K£Æ
£®1£©»ÁÕº1£¨«Û÷§£∫KE=GE£ª
£®2£©»ÁÕº2£¨¡¨Ω”CABG£¨»Ù°œFGB=![]() °œACH£¨«Û÷§£∫CA°ŒFE£ª
°œACH£¨«Û÷§£∫CA°ŒFE£ª
£®3£©»ÁÕº3£¨‘⁄£®2£©µƒÃıº˛œ¬£¨¡¨Ω”CGΩªAB”⁄µ„N£¨»ÙsinE=![]() £¨AK=
£¨AK=![]() £¨«ÛCNµƒ≥§£Æ
£¨«ÛCNµƒ≥§£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄![]() ÷–£¨
÷–£¨![]() ¥π÷±∆Ω∑÷
¥π÷±∆Ω∑÷![]() £¨∑÷±Ωª
£¨∑÷±Ωª![]() °¢
°¢![]() ”⁄µ„
”⁄µ„![]() °¢
°¢![]() £¨
£¨![]() ¥π÷±∆Ω∑÷
¥π÷±∆Ω∑÷![]() £¨∑÷±Ωª
£¨∑÷±Ωª![]() £¨
£¨![]() ”⁄µ„
”⁄µ„![]() °¢
°¢![]() £Æ
£Æ
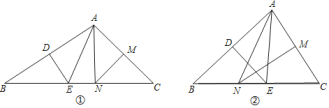
£®1£©«Î≈–∂œ°˜ANEµƒ÷Ð≥§”ÎAB+ACµƒ∫Õµƒ¥Û–°,≤¢Àµ√˜¿Ì”….
£®2£©¢Ÿ»ÁÕº¢Ÿ£¨»Ù°œB=34°„£¨°œC=28°„£¨«Û![]() µƒ∂» ˝Œ™______£ª
µƒ∂» ˝Œ™______£ª
¢⁄»ÁÕº¢⁄£¨»Ù![]() £¨‘Ú
£¨‘Ú![]() µƒ∂» ˝Œ™________£ª
µƒ∂» ˝Œ™________£ª
¢€»Ù![]()
![]() £¨‘Ú
£¨‘Ú![]() µƒ∂» ˝Œ™________.
µƒ∂» ˝Œ™________.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∂˛¥Œ∫Ø ˝y=ax2+bx+cµƒÕºœÛ∑÷±æ≠π˝µ„£®0£¨3£©£¨£®3£¨0£©£¨£®4£¨©Å5£©£Æ
£®1£©«Û’‚∏ˆ∂˛¥Œ∫Ø ˝µƒΩ‚Œˆ Ω£ª
£®2£©«Û’‚∏ˆ∂˛¥Œ∫Ø ˝µƒ◊Ó÷µ£ª
£®3£©»Ù…Ë’‚∏ˆ¥Œ∫Ø ˝ÕºœÛ”Îx÷·Ωª”⁄µ„C£¨D£®µ„C‘⁄µ„Dµƒ◊Û≤ý£©£¨«“µ„A «∏√ÕºœÛµƒ∂•µ„£¨«Î‘⁄’‚∏ˆ∂˛¥Œ∫Ø ˝µƒ∂‘≥∆÷·…œ»∑∂®“ªµ„B£¨ π°˜ACB ±µ»—¸»˝Ω«–Œ£¨«Û≥ˆµ„Bµƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕºÀ˘ 棨![]() £¨Ω·¬€£∫¢Ÿ
£¨Ω·¬€£∫¢Ÿ![]() £ª¢⁄
£ª¢⁄![]() £ª¢€
£ª¢€![]() £ª¢Ð
£ª¢Ð![]() £¨∆‰÷–’˝»∑µƒ «”–£® £©
£¨∆‰÷–’˝»∑µƒ «”–£® £©
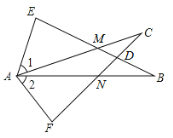
A.1∏ˆB.2∏ˆC.3∏ˆD.4∏ˆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
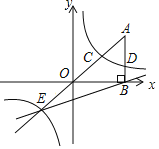
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨Aµ„µƒ◊¯±ÍŒ™£®a£¨6£©£¨AB°Õx÷·”⁄µ„B£¨cos°œOAB®T![]() £¨∑¥±»¿˝∫Ø ˝y=
£¨∑¥±»¿˝∫Ø ˝y=![]() µƒÕºœÛµƒ“ª÷ß∑÷±ΩªAO°¢AB”⁄µ„C°¢D£Æ—”≥§AOΩª∑¥±»¿˝∫Ø ˝µƒÕºœÛµƒ¡Ì“ª÷ß”⁄µ„E£Æ“—÷™µ„Dµƒ◊ð◊¯±ÍŒ™
µƒÕºœÛµƒ“ª÷ß∑÷±ΩªAO°¢AB”⁄µ„C°¢D£Æ—”≥§AOΩª∑¥±»¿˝∫Ø ˝µƒÕºœÛµƒ¡Ì“ª÷ß”⁄µ„E£Æ“—÷™µ„Dµƒ◊ð◊¯±ÍŒ™![]() £Æ
£Æ
£®1£©«Û∑¥±»¿˝∫Ø ˝µƒΩ‚Œˆ Ω£ª
£®2£©«Û÷±œþEBµƒΩ‚Œˆ Ω£ª
£®3£©«ÛS°˜OEB£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com