
����Ŀ����֪����������![]() ���㣬��
���㣬��![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() ����
����![]() ��
��![]() �����ߣ���
�����ߣ���![]() ������һ����
������һ����![]() �������ϵ�
�������ϵ�![]() ��������ÿ��
��������ÿ��![]() ����λ���ȵ��ٶ����������������˶�������
����λ���ȵ��ٶ����������������˶�������![]() �ӵ�
�ӵ�![]() ��������ÿ��
��������ÿ��![]() ���� λ���ȵ��ٶ������������������˶������˶�ʱ��Ϊ
���� λ���ȵ��ٶ������������������˶������˶�ʱ��Ϊ![]() �룬����������⣺
�룬����������⣺
![]() д�������ϵ�
д�������ϵ�![]() ����ʾ������
����ʾ������
![]() ����
����![]() �ֱ��
�ֱ��![]() ����ͬʱ�������ʵ�
����ͬʱ�������ʵ�![]() �˶����������
�˶����������![]() ���
���![]() ����λ���ȣ�
����λ���ȣ�
![]() ̽�����⣺��
̽�����⣺��![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() Ϊ
Ϊ![]() ���е㣬����
���е㣬����![]() ���߶�
���߶�![]() ���˶������У�̽���߶�
���˶������У�̽���߶�![]() ���߶�
���߶�![]() ��������ϵ��д�����̣���
��������ϵ��д�����̣���

���𰸡���1��-4����2��![]() ���
���![]() ��ʱ���
��ʱ���![]() ����λ����3��
�������3��![]() ��
��![]() �Ҳ࣬
�Ҳ࣬![]() ��
��![]() ��
��![]() ��࣬
��࣬![]()
��������
��1��������֪�ɵ�B���ʾ����Ϊ8-12��
��2����P�˶�x��ʱ����Q���2����λ���ȣ���AP=3x��BQ=2x������AP+BQ=AB-3����AP+BQ=AB+3���г�������⼴�ɣ�
��3�����ݵ�P�ڵ�A��B����֮���˶�����MN=MQ+NP-PQ���ɴ˿ɵó����ۣ�
��1���١ߵ�A��ʾ����Ϊ8��B��A����ߣ�AB=12��
���B��ʾ������8-12=-4��
��2�����P�˶�x��ʱ����Q���3����λ���ȣ�![]()
��AP=3x��BQ=2x��
��AP+BQ=AB-3��
��3x+2x=9��
��ã�x=1.8��![]()
��AP+BQ=AB+3��
��3x+2x=15
��ã�x=3��
���P�˶�1.8���3��ʱ���Q���3����λ���ȣ�
��3��2MN+PQ=12��2MN-PQ=12���������£�![]()
P��Q�Ҳ�ʱ�У�MN=MQ+NP-PQ=![]() AQ+
AQ+![]() BP-PQ=
BP-PQ=![]() ��AQ+BP-PQ��-
��AQ+BP-PQ��-![]() PQ=
PQ=![]() AB-
AB-![]() PQ=
PQ=![]() ��12-PQ����
��12-PQ����
��2MN+PQ=12��
ͬ��P��Q���ʱ�У�2MN-PQ=12��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
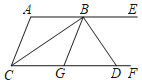
����Ŀ����ͼ��AE��CF����ACF��ƽ���߽�AE�ڵ�B��G��CF�ϵ�һ�㣬��GBE��ƽ���߽�CF�ڵ�D����BD��BC�����н��ۣ���BCƽ�֡�ABG����AC��BG�������DBE����Ľ���2����������A���������BDF��![]() ��������ȷ����_____����������Ϊ��ȷ���۵���Ŷ����ϣ�
��������ȷ����_____����������Ϊ��ȷ���۵���Ŷ����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����DAC����EBC���ǵȱ������Σ���A��C��B��ͬһ��ֱ���ϣ���AE��BD�ֱ���CD��CE���ڵ�M��N.

��֤����1��AE=DB��
��2����CMNΪ�ȱ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
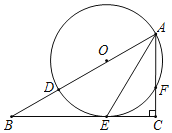
����Ŀ����ͼ����Rt��ABC�У���C=90������D���߶�AB�ϣ���ADΪֱ���ġ�O��BC�ཻ�ڵ�E����AC�ཻ�ڵ�F����B=��BAE=30�㣮
��1����֤��BC�ǡ�O�����ߣ�
��2����AC=3�����O�İ뾶r��
��3���ڣ�1���������£��ж���A��O��E��FΪ������ı���Ϊ���������ı��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ס���ṹ��ͼ��ʾ��С���������ҺͿ�������ľ�ذ�.
(1)������������Ҫ�����ƽ����ľ�ذ壿(����ĸ��ʾ)
(2)��![]() �ף�
�ף�![]() ��ʱ������ÿƽ����ľ�ذ�ļ۸���
��ʱ������ÿƽ����ľ�ذ�ļ۸���![]() Ԫ������������Ҫ������ԪǮ��
Ԫ������������Ҫ������ԪǮ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ҹ��Ŵ���һ���Գ���ϵ����ѧר���������˶�����ѧ����߳ɾͣ������㷨��ϵ���������ƶ��ż�����ķ�չ��Ӧ�ã����м��أ�������Բ�����ڱ��У���֪��С���Ծ��֮����һ�磬�����һ�ߣ��ʾ����Σ�����Ϊ��������һԲ����ľ�ģ�����ǽ���У���֪���С���þ�ȥ����ľ�ģ������1�磨ED=1�磩�������1�ߣ�AB=1��=10�磩���������Բ��ľ�ĵ�ֱ���Ƕ��٣���
��ͼ��ʾ���������ѧ֪ʶ���㣺Բ��ľ�ĵ�ֱ��AC�ǣ�������
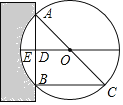
A. 13�� B. 20�� C. 26�� D. 28��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���mx2+��1��5m��x��5=0��m��0����
��1����֤������mΪ�κη���ʵ�����˷�����������ʵ������
��2����������y=mx2+��1��5m��x��5��x�ύ��A��x1��0����B��x2��0�����㣬��|x1��x2|=6����m��ֵ��
��3����m��0����P��a��b����Q��a+n��b���ڣ�2���е��������ϣ���P��Q���غϣ��������ʽ4a2��n2+8n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڡ�ABC�У�AB=8cm��AC=4cm����BAC��ƽ����AD��BC�Ĵ�ֱƽ����DG���ڵ�D������D��ֱ��DE��AB�ڵ�E��DF��AC�ڵ�F.
��1����֤��BE=CF��
��2����AE�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ѧ����ϣ���ʦ��ͬѧ�ǵ��ٳ��ϲ�����˵ĸ߶ȣ�Ȼ������������ԵIJ���������С���IJ��������ǣ���һ����3.5�����ֱ���������27��C������ͼ����Ȼ����BC�����ߵ�D������ʱĿ����˶���A����Ͷ���Eǡ����ͬһֱ���ϣ��ֲ��C��D����ľ���Ϊ3�ף�С����Ŀ��Ϊ1.5�ף��������֪����˵ĸߣ�����Ϊ���ֲ��������Ƿ���У���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com