
【题目】如图,在Rt△ABC中,∠C=90°,点D在线段AB上,以AD为直径的⊙O与BC相交于点E,与AC相交于点F,∠B=∠BAE=30°.
(1)求证:BC是⊙O的切线;
(2)若AC=3,求⊙O的半径r;
(3)在(1)的条件下,判断以A、O、E、F为顶点的四边形为哪种特殊四边形,并说明理由.
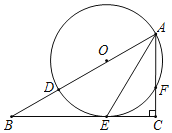
【答案】(1)证明见解析;(2)⊙O的半径为2;(3)四边形OAFE是菱形,理由见解析.
【解析】(1)利用等腰三角形的性质和三角形外角的性质得出∠AOE=60°,进而得出∠BEO=90°,即可得出结论;
(2)先求出∠AEC=60°,利用锐角三角函数求出AE,最后用三角函数即可得出结论;
(3)先判断出△AOF是等边三角形,得出OA=AF,∠AOF=60°,进而判断出△OEF是等边三角形,即可判断出四边相等,即可得出结论.
(1)如图1,
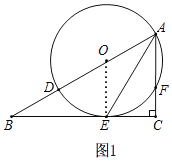
连接OE,∴OA=OE,
∴∠BAE=∠OEA,
∵∠BAE=30°,
∴∠OEA=30°,
∴∠AOE=∠BAE+∠OEA=60°,
在△BOE中,∠B=30°,
∴∠OEB=180°-∠B-∠BOE=90°,
∴OE⊥BC,
∵点E在⊙O上,
∴BC是⊙O的切线;
(2)如图2,
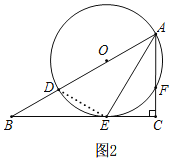
∵∠B=∠BAE=30°,
∴∠AEC=∠B+∠BAE=60°,
在Rt△ACE中,AC=3,sin∠AEC=![]() ,
,
∴AE=![]() ,
,
连接DE,∵AD是⊙O的直径,
∴∠AED=90°,
在Rt△ADE中,∠BAE=30°,cos∠DAE=![]() ,
,
∴AD=![]() ,
,
∴⊙O的半径r=![]() AD=2;
AD=2;
(3)以A、O、E、F为顶点的四边形是菱形,理由:如图3,
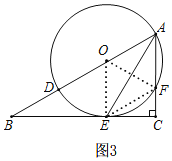
在Rt△ABC中,∠B=30°,
∴∠BAC=60°,
连接OF,∴OA=OF,
∴△AOF是等边三角形,
∴OA=AF,∠AOF=60°,
连接EF,OE,
∴OE=OF,
∵∠OEB=90°,∠B=30°,
∴∠AOE=90°+30°=120°,
∴∠EOF=∠AOE-∠AOF=60°,
∵OE=OF,
∴△OEF是等边三角形,
∴OE=EF,
∵OA=OE,
∴OA=AF=EF=OE,
∴四边形OAFE是菱形.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
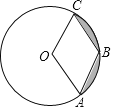
【题目】如图,已知⊙O的半径是2,点A、B、C在⊙O上,若四边形OABC为菱形,则图中阴影部分面积为( )
A. ![]() π﹣2
π﹣2![]() B.
B. ![]() π﹣
π﹣![]() C.
C. ![]() π﹣2
π﹣2![]() D.
D. ![]() π﹣
π﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A,B两点,分别表示﹣40,20,甲、乙两只蚂蚁分别从A,B两点同时出发,甲沿线段AB方向以3个单位长度/秒的速度向右运动,甲到达点B处时运动停止;乙沿线段BA方向以5个单位长度/秒的速度向左运动.
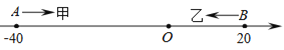
(1)求甲、乙第一次相遇点所表示的数.
(2)求经过多少秒时,甲、乙相距28个单位长度?
(3)若乙到达A点后立刻掉头追赶甲(速度保持不变),则在甲到达B点前,甲、乙是否还能再次相遇?若能,求出相遇点所表示的数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家计划平均每天销售滑板车100辆,但实际的销售量与计划量有出入,下表是某周的销售情况(超额记为正,不足记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划数的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知该商家前三天共销售滑板车______辆;(直接写答案)
(2)根据记录的数据可知销售量最多的一天比销售量最少的-天多销售多少辆?
(3)本周实际销售量是多少?
(4)该商家实行每周计件工资制,每销售一辆车可得40元,若超额完成任务,则超过部分每辆另奖20元,少销售一辆扣25元,那么该商家的销售人员这一周的工资总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
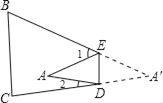
【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
(1)设∠AED的度数为x,∠ADE的度数为y,那么∠1、∠2的度数分别是多少?(用含有x或y的代数式表示)
(2)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
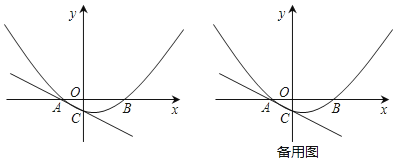
【题目】如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣![]() x﹣1交于点C.
x﹣1交于点C.
(1)求抛物线解析式及对称轴;
(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO的周长最小?若存在,求出点P的坐标,若不存在,请说明理由;
(3)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在数轴上有![]() 两点,点
两点,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 在
在![]() 点的左边,且
点的左边,且![]() .若有一动点
.若有一动点![]() 从数轴上点
从数轴上点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向左匀速运动,动点
个单位长度的速度沿数轴向左匀速运动,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单 位长度的速度沿着数轴向右匀速运动,设运动时间为
个单 位长度的速度沿着数轴向右匀速运动,设运动时间为![]() 秒,解决以下问题:
秒,解决以下问题:
![]() 写出数轴上点
写出数轴上点![]() 所表示的数;
所表示的数;
![]() 若点
若点![]() 分别从
分别从![]() 两点同时出发,问点
两点同时出发,问点![]() 运动多少秒与点
运动多少秒与点![]() 相距
相距![]() 个单位长度?
个单位长度?
![]() 探索问题:若
探索问题:若![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,当点
的中点,当点![]() 在线段
在线段![]() 上运动过程中,探索线段
上运动过程中,探索线段![]() 与线段
与线段![]() 的数量关系(写出过程).
的数量关系(写出过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
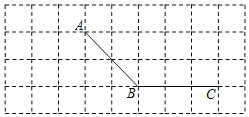
【题目】如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.
![]() 过点C画线段AB的平行线CD;
过点C画线段AB的平行线CD;
![]() 过点A画线段BC的垂线,垂足为E;
过点A画线段BC的垂线,垂足为E;
![]() 过点A画线段AB的垂线,交线段CB的延长线于点F;
过点A画线段AB的垂线,交线段CB的延长线于点F;
![]() 线段AE的长度是点______到直线______的距离;
线段AE的长度是点______到直线______的距离;
![]() 线段AE、BF、AF的大小关系是______
线段AE、BF、AF的大小关系是______![]() 用“
用“![]() ”连接
”连接![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com