
����Ŀ����֪��������A��B���㣬�ֱ��ʾ��40��20���ס�����ֻ���Ϸֱ��A��B����ͬʱ�����������߶�AB������3����λ����/����ٶ������˶��������B��ʱ�˶�ֹͣ�������߶�BA������5����λ����/����ٶ������˶���
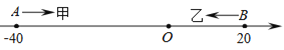
��1����ס��ҵ�һ������������ʾ������
��2����������ʱ���ס������28����λ���ȣ�
��3�����ҵ���A������̵�ͷ�ϼף��ٶȱ��ֲ��䣩�����ڼ���B��ǰ���ס����Ƿ����ٴ����������ܣ��������������ʾ�����������ܣ���˵�����ɣ�
���𰸡���1���ס��ҵ�һ���������ʾ������![]() ����2������4���11��ʱ���ס������28����λ���ȣ���3���ס��Ҳ����ٴ����������ɼ�����
����2������4���11��ʱ���ס������28����λ���ȣ���3���ס��Ҳ����ٴ����������ɼ�����
��������
��1�����������֪����һ������ʱ���������ߵ���·��Ϊ60���ݴ˽�һ���������ʱ�䲢�г������������ʱ�䣬Ȼ���һ�����㼴�ɣ�
��2���辭��y��ʱ�ס������28����λ���ȣ�Ȼ�������ǰ�����������������һ���������г�������⼴�ɣ�
��3����ס����ٴ���������ʻ![]() �룬Ȼ����������г����̣������ʱ��ʱ�䣬�ݴ��������ʻ·�̣������������жϼ���.
�룬Ȼ����������г����̣������ʱ��ʱ�䣬�ݴ��������ʻ·�̣������������жϼ���.
��1����ס��Ҿ���![]() ���һ��������
���һ��������
��![]() ��
��
��ã�![]() ��
��
��40+![]() =
=![]() ��
��
�𣺼ס��ҵ�һ���������ʾ������![]() ��
��
��2���辭��y��ʱ�ס������28����λ���ȣ�
��3y+5y=6028��3y+5y60=28��
��ã�y=4��y=11��
�𣺾���4���11��ʱ���ס������28����λ���ȣ�
��3������B��ǰ���ס��Ҳ����ٴ�������
�������£�
��ס����ٴ���������ʻ![]() �룬
�룬
��![]() ��
��
��ã�![]() ��
��
��![]() ,
,
��ס��Ҳ����ٴ�����.


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪n���ε��ڽǺ���=��n-2����180��.
��1����ͬѧ˵������ȡ360��������ͬѧ˵����Ҳ��ȡ630��.�ס��ҵ�˵���������ԣ��������n.�����ԣ�˵�����ɣ�
��2����n���α�Ϊ��n+x�����Σ������ڽǺ�������360�������з��̵ķ���ȷ��x.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AE��CF����ACF��ƽ���߽�AE�ڵ�B��G��CF�ϵ�һ�㣬��GBE��ƽ���߽�CF�ڵ�D����BD��BC�����н��ۣ���BCƽ�֡�ABG����AC��BG�������DBE����Ľ���2����������A���������BDF��![]() ��������ȷ����_____����������Ϊ��ȷ���۵���Ŷ����ϣ�
��������ȷ����_____����������Ϊ��ȷ���۵���Ŷ����ϣ�
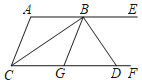
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪��������ĸ��ʾ�Ĵ���ʽ�Ǿ���һ������ģ����и���3aʵ������������в���ȷ���ǣ� ��
A.��a��ʾһ���ȱ������εı߳�����3a��ʾ����ȱ������ε��ܳ�
B.��ƻ���ļ۸���3Ԫ/ǧ�ˣ���3a��ʾ��aǧ��ƻ���Ľ��
C.��һ����λ����ʮλ������3��λ������a����3a��ʾ�����λ��
D.��һ��Բ����ĵ������3������a����3a��ʾ���Բ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����⣩
��֪�����ǰ�һ���������е�һ�����������������ĸ����ĺͶ���ȣ��������ݴ�ǰ���ӵ�һ������ʼ�����ǣ�5����2��1��9��x������
������Ӧ�ã�
��1�����5����x��
��2�����ǰ����ǰ38�����ĺͣ�
��3����mΪ��������ֱ���ú�m��ʽ�ӱ�ʾ���֣�2���ڵڼ�������λ���ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O��ֱ����P��BA�ӳ�����һ�㣬PC�С�O�ڵ�C��CG�ǡ�O���ң�CG��AB������ΪD��
��1����֤����PCA=��ABC��
��2������A��AE��PC����O�ڵ�E����CD�ڵ�F������BE����cos��P=![]() ��CF=10����BE�ij�
��CF=10����BE�ij�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����DAC����EBC���ǵȱ������Σ���A��C��B��ͬһ��ֱ���ϣ���AE��BD�ֱ���CD��CE���ڵ�M��N.

��֤����1��AE=DB��
��2����CMNΪ�ȱ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90������D���߶�AB�ϣ���ADΪֱ���ġ�O��BC�ཻ�ڵ�E����AC�ཻ�ڵ�F����B=��BAE=30�㣮
��1����֤��BC�ǡ�O�����ߣ�
��2����AC=3�����O�İ뾶r��
��3���ڣ�1���������£��ж���A��O��E��FΪ������ı���Ϊ���������ı��Σ���˵�����ɣ�
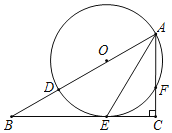
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڡ�ABC�У�AB=8cm��AC=4cm����BAC��ƽ����AD��BC�Ĵ�ֱƽ����DG���ڵ�D������D��ֱ��DE��AB�ڵ�E��DF��AC�ڵ�F.
��1����֤��BE=CF��
��2����AE�ij�.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com