【题目】（阅读理解）
已知下面是按一定规律排列的一列数，且任意相邻四个数的和都相等．这列数据从前往后，从第一个数开始依次是－5，－2，1，9，x，…．
（理解应用）
（1）求第5个数x；
（2）求从前往后前38个数的和；
（3）若m为正整数，直接用含m的式子表示数字－2处在第几个数的位置上．
【答案】（1）
；（2）从前往后前38个数的和是20；（3）数字－2处在第
个数的位置上
【解析】
（1）根据“任意相邻四个数的和都相等”列出方程，然后进一步求解即可；
（2）求出
的值后，进一步观察这列数字可知它们每4个数一循环，据此进一步求解即可；
（3）结合（1）、（2）总结出这列数字的规律，然后进一步归纳即可.
（1）由题意，得：
，
∴
（2）由（1）可得，这列数字为：
…
∵任意相邻四个数的和都相等，
∴这列数字每4个数一循环，
∵
，
∴
，
即从前往后前38个数的和是20；
（3）结合（1）、（2）可知：
该列数字为：
…
∴数字
所在的位置为第二个数、第六个数、第十个数……
∵
，
，
…
∴数字－2处在第个数的位置上.
导学全程练创优训练系列答案科目：初中数学 来源： 题型：
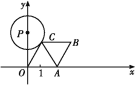
【题目】如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,经过t秒后,以O,A为顶点作菱形OABC,使B,C点都在第一象限内,且AO=AC,又以P(0,4
)为圆心,PC为半径的圆恰好与OC所在的直线相切,则t等于( )
A. 2-1 B. 2+1 C. 5 D. 7
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】△ABC中，AB=AC=12厘米，∠B=∠C，BC=8厘米，点D为AB的中点．如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．若点Q的运动速度为_____厘米/秒，△BPD与△CQP全等.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在三角形ABC中，D是BC上一点，且∠CDA＝∠CAB．（注：三角形内角和等于180°）
（1）求证：∠CDA＝∠DAB+∠DBA；
（2）如图2，MN是经过点D的一条直线，若直线MN交AC边于点E，且∠CDE＝∠CAD．求证：∠AED+∠EAB＝180°；
（3）将图2中的直线MN绕点D旋转，使它与射线AB交于点P（点P不与点A，B重合）．在图3中画出直线MN，并用等式表示∠CAD，∠BDP，∠BPD这三个角之间的数量关系，不需证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
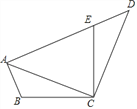
【题目】如图，已知在四边形ABCD中，点E在AD上，∠BCE=∠ACD=90°,∠BAC=∠D，BC=CE．
（1）求证：AC=CD；
（2）若∠ACB=30°，∠D=45°,求∠AEC的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知数轴上有A，B两点，分别表示﹣40，20，甲、乙两只蚂蚁分别从A，B两点同时出发，甲沿线段AB方向以3个单位长度/秒的速度向右运动，甲到达点B处时运动停止；乙沿线段BA方向以5个单位长度/秒的速度向左运动．
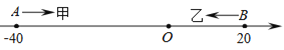
（1）求甲、乙第一次相遇点所表示的数．
（2）求经过多少秒时，甲、乙相距28个单位长度？
（3）若乙到达A点后立刻掉头追赶甲（速度保持不变），则在甲到达B点前，甲、乙是否还能再次相遇？若能，求出相遇点所表示的数；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】解下列方程:
(1)x2+8x-20=0(用配方法);
(2)x2-2x-3=0;
(3)(x-1)(x+2)=4(x-1);
(4)3x2-6x=1(用公式法).
查看答案和解析>>
科目：初中数学 来源： 题型：
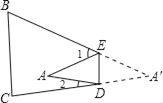
【题目】如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，
（1）设∠AED的度数为x，∠ADE的度数为y，那么∠1、∠2的度数分别是多少？（用含有x或y的代数式表示）
（2）∠A与∠1+∠2之间有一种数量关系始终保持不变，请找出这个规律，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】垃圾的分类处理与回收利用，可以减少污染，节省资源．某城市环保部门为了提高宣传实效，抽样调查了部分居民小区一段时间内生活垃圾的分类情况，其相关信息如下：
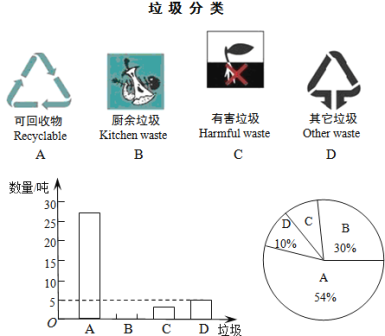
根据图表解答下列问题：
（1）请将条形统计图补充完整；
（2）在扇形统计图样中，产生的有害垃圾C所对应的圆心角 度；
（3）调查发现，在可回收物中塑料类垃圾占13%，每回收1吨塑料类垃圾可获得0.5吨二级原料．假设该城市每月产生的生活垃圾为1000吨，且全部分类处理，那么每月回收的塑料类垃圾可以获得多少吨二级原料？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com