
ЁОЬтФПЁПРЌЛјЕФЗжРрДІРэгыЛиЪеРћгУЃЌПЩвдМѕЩйЮлШОЃЌНкЪЁзЪдДЃЎФГГЧЪаЛЗБЃВПУХЮЊСЫЬсИпаћДЋЪЕаЇЃЌГщбљЕїВщСЫВПЗжОгУёаЁЧјвЛЖЮЪБМфФкЩњЛюРЌЛјЕФЗжРрЧщПіЃЌЦфЯрЙиаХЯЂШчЯТЃК
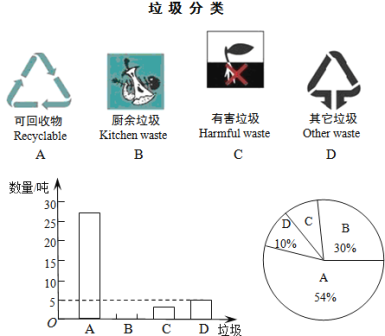
ИљОнЭМБэНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧыНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉдкЩШаЮЭГМЦЭМбљжаЃЌВњЩњЕФгаКІРЌЛјCЫљЖдгІЕФдВаФНЧ ЖШЃЛ
ЃЈ3ЃЉЕїВщЗЂЯжЃЌдкПЩЛиЪеЮяжаЫмСЯРрРЌЛјеМ13%ЃЌУПЛиЪе1ЖжЫмСЯРрРЌЛјПЩЛёЕУ0.5ЖжЖўМЖдСЯЃЎМйЩшИУГЧЪаУПдТВњЩњЕФЩњЛюРЌЛјЮЊ1000ЖжЃЌЧвШЋВПЗжРрДІРэЃЌФЧУДУПдТЛиЪеЕФЫмСЯРрРЌЛјПЩвдЛёЕУЖрЩйЖжЖўМЖдСЯЃП
ЁОД№АИЁПЃЈ1ЃЉЭММћНтЮіЃЛЃЈ2ЃЉ21.6ЃЛЃЈ3ЃЉ35.1ЖжЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШИљОнЬѕаЮЭМКЭЩШаЮЭМЧѓГіРЌЛјзмЪ§ЃЌМДПЩЕУГіГјгрРЌЛјBЕФЪ§СПЃЌНјЖјМДПЩВЙШЋЬѕаЮЭМЃЛ
ЃЈ2ЃЉЯШЧѓГігаКІРЌЛјCЫљеМЕФАйЗжБШЃЌШЛКѓМДПЩЕУГіЦфЫљЖдЕФдВаФНЧЃЛ
ЃЈ3ЃЉЯШЧѓГіПЩЛиЪеЮяжаЫмСЯРрРЌЛјЕФЪ§СПЃЌШЛКѓМДПЩЕУГіЖўМЖдСЯЕФЪ§СП.
ЃЈ1ЃЉгЩЬтвтЃЌЕУ
РЌЛјзмЪ§ЮЊЃК![]() ЃЈЖжЃЉ
ЃЈЖжЃЉ
ЁрГјгрРЌЛјBЕФЪ§СПЮЊЃК![]() ЃЈЖжЃЉ
ЃЈЖжЃЉ
ВЙШЋЬѕаЮЭМШчЯТЃК
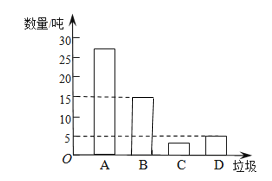
ЃЈ2ЃЉгаКІРЌЛјCЫљеМЕФАйЗжБШЮЊЃК![]()
ЁргаКІРЌЛјCЫљЖдгІЕФдВаФНЧЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉгЩЬтвтЃЌЕУ
![]() Жж
Жж
Д№ЃКУПдТЛиЪеЕФЫмСЯРрРЌЛјПЩвдЛёЕУ35.1ЖжЖўМЖдСЯ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓгыЗДБШР§КЏЪ§
ЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЃЈ
ЃЈ![]() ЮЊГЃЪ§Чв
ЮЊГЃЪ§Чв![]() ЃЉЕФЭМЯѓНЛгк
ЃЉЕФЭМЯѓНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() .
.
ЃЈ1ЃЉЧѓДЫЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉШєЕу![]() дк
дк![]() жсЩЯЃЌЧв
жсЩЯЃЌЧв![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФзјБъ.
ЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОиаЮЃЈЗЧе§ЗНаЮЃЉЫФИіФкНЧЕФЦНЗжЯпЮЇГЩЕФЫФБпаЮЪЧ__________аЮ.ЃЈлњЬиЪтЫФБпаЮЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ ![]() ЪЧвд
ЪЧвд![]() ЮЊжБОЖЕФ
ЮЊжБОЖЕФ![]() ЩЯЕФЕуЃЌ
ЩЯЕФЕуЃЌ![]() ЃЌЯв
ЃЌЯв![]() НЛ
НЛ![]() гкЕу
гкЕу![]() .
.
(1)ЕБ![]() ЪЧ
ЪЧ![]() ЕФЧаЯпЪБЃЌЧѓжЄ:
ЕФЧаЯпЪБЃЌЧѓжЄ: ![]() ЃЛ
ЃЛ
(2)ЧѓжЄ: ![]() ЃЛ
ЃЛ
(3)вбжЊ![]() ЃЌ
ЃЌ![]() ЪЧАыОЖ
ЪЧАыОЖ![]() ЕФжаЕуЃЌЧѓЯпЖЮ
ЕФжаЕуЃЌЧѓЯпЖЮ![]() ЕФГЄ.
ЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌФГЙЋдАЩшМЦНкШеЯЪЛЈАкЗХЗНАИЃЌЦфжавЛИіЛЈЬГгЩвЛХњЛЈХшЖбГЩСљНЧЖтЃЌЖЅВувЛИіЃЌвдЯТИїВуЖбГЩСљБпаЮЃЌж№ВуУПБпдіМгвЛИіЛЈХшЃЌШєетЖтЛЈХшЕзВузюГЄЕФвЛХХЙВ13ИіЛЈХшЃЌдђЕзВуЕФЛЈХшЕФИіЪ§ЪЧЃЈ ЃЉ
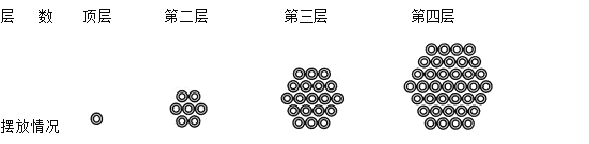
A.91B.127C.169D.255
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
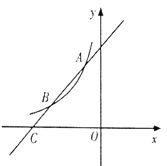
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() ЕФЖЅЕуЮЊBЃЈ-1ЃЌ3ЃЉЃЌгы
ЕФЖЅЕуЮЊBЃЈ-1ЃЌ3ЃЉЃЌгы![]() жсЕФНЛЕуAдкЕуЃЈ-3ЃЌ0ЃЉКЭЃЈ-2ЃЌ0ЃЉжЎМфЃЌвдЯТНсТлЃКЂй
жсЕФНЛЕуAдкЕуЃЈ-3ЃЌ0ЃЉКЭЃЈ-2ЃЌ0ЃЉжЎМфЃЌвдЯТНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЃЛ Ђн
ЃЛ Ђн![]() Цфжае§ШЗЕФгаЃЈЁЁЁЁЃЉ
Цфжае§ШЗЕФгаЃЈЁЁЁЁЃЉ
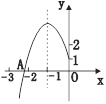
A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаЕчЛАВІКХЩЯЭјгаСНжжЪеЗбЗНЪНЃЌгУЛЇПЩвдШЮбЁЦфвЛЃКAЁЂМЦЪБжЦЃК0ЃЎ05дЊ/ЗжжгЃЛBЁЂдТзтжЦЃК50дЊ/дТЃЈЯовЛВПИіШЫзЁеЌЕчЛАЩЯЭјЃЉЃЎДЫЭтЃЌУПжжЩЯЭјЗНЪНЖМЕУМгЪеЭЈаХЗб0ЃЎ02дЊ/ЗжжгЃЎ
ЃЈ1ЃЉаЁСсЫЕЃКСНжжМЦЗбЗНЪНЕФЪеЗбЖдЫ§РДЫЕЪЧвЛбљЕФЃЎаЁСсУПдТЩЯЭјЖрЩйаЁЪБЃП
ЃЈ2ЃЉФГгУЛЇЙРМЦвЛИідТФкЩЯЭјЕФЪБМфЮЊ65аЁЪБЃЌФуШЯЮЊВЩгУФФжжЗНЪННЯЮЊКЯЫуЃПЮЊЪВУДЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
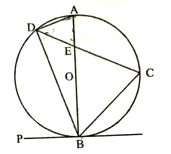
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпy=Љx2+bx+cОЙ§AЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉСНЕуЃЌгыyжсЯрНЛгкЕуCЃЌСЌНсBCЃЌЕуPЮЊХзЮяЯпЩЯвЛЖЏЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпlЃЌНЛжБЯпBCгкЕуGЃЌНЛxжсгкЕуEЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉЕБPЮЛгкyжсгвБпЕФХзЮяЯпЩЯдЫЖЏЪБЃЌЙ§ЕуCзїCFЁЭжБЯпlЃЌFЮЊДЙзуЃЌЕБЕуPдЫЖЏЕНКЮДІЪБЃЌвдPЃЌCЃЌFЮЊЖЅЕуЕФШ§НЧаЮгыЁїOBCЯрЫЦЃПВЂЧѓГіДЫЪБЕуPЕФзјБъЃЛ

ЃЈ3ЃЉШчЭМ2ЃЌЕБЕуPдкЮЛгкжБЯпBCЩЯЗНЕФХзЮяЯпЩЯдЫЖЏЪБЃЌСЌНсPCЃЌPBЃЌЧыЮЪЁїPBCЕФУцЛ§SФмЗёШЁЕУзюДѓжЕЃПШєФмЃЌЧыЧѓГізюДѓУцЛ§SЃЌВЂЧѓГіДЫЪБЕуPЕФзјБъЃЌШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЈaЪЧГЃЪ§ЃЌaЁй0ЃЉЃЌЯТСаНсТле§ШЗЕФЪЧЃЈ ЃЉ
ЃЈaЪЧГЃЪ§ЃЌaЁй0ЃЉЃЌЯТСаНсТле§ШЗЕФЪЧЃЈ ЃЉ
AЃЎЕБa=1ЪБЃЌКЏЪ§ЭМЯѓОЙ§ЕуЃЈЉ1ЃЌ1ЃЉ
BЃЎЕБa=Љ2ЪБЃЌКЏЪ§ЭМЯѓгыxжсУЛгаНЛЕу
CЃЎШєaЃМ0ЃЌКЏЪ§ЭМЯѓЕФЖЅЕуЪМжедкxжсЕФЯТЗН
DЃЎШєaЃО0ЃЌдђЕБxЁн1ЪБЃЌyЫцxЕФдіДѓЖјдіДѓ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com