
【题目】如图, ![]() 是以
是以![]() 为直径的
为直径的![]() 上的点,
上的点,![]() ,弦
,弦![]() 交
交![]() 于点
于点![]() .
.
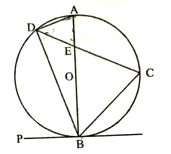
(1)当![]() 是
是![]() 的切线时,求证:
的切线时,求证: ![]() ;
;
(2)求证: ![]() ;
;
(3)已知![]() ,
,![]() 是半径
是半径![]() 的中点,求线段
的中点,求线段![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(3)DE=![]()
【解析】(1)由AB是直径,可得∠DAB+∠ABD=90°,再根据 PB是⊙O的切线,可得∠ABD+∠PBD=90°,根据同角的余角相等即可证得∠PBD=∠DAB;
(2)证明△BCE∽△DCB,根据相似三角形对应边成比例可得BC2=CECD,再根据CD=CE+DE经过推导即可得BC2- CE2= CEDE;
(3) 连接OC,由![]() ,AB是直径,可得∠AOC=∠BOC=90°,根据勾股定理则有CE=OE+CO, BC=OB+CO ,再根据OA=4 ,E 是半径 OA 的中点,继而可得BC=4
,AB是直径,可得∠AOC=∠BOC=90°,根据勾股定理则有CE=OE+CO, BC=OB+CO ,再根据OA=4 ,E 是半径 OA 的中点,继而可得BC=4![]() ,CE=2
,CE=2![]() ,再根据(2)中 BC-CE=CE·DE,即可求得DE的长.
,再根据(2)中 BC-CE=CE·DE,即可求得DE的长.
(1)∵AB是直径,
∴∠ADB=90°,即∠DAB+∠ABD=90°,
又 ∵ PB是⊙O的切线,
∴PB⊥AB,
∴∠ABP=90°,即∠ABD+∠PBD=90°,
∴∠PBD=∠DAB;
(2)∵![]() ,
,
∴∠BDC=∠EBC,
又∵∠BCE=BCD,
∴△BCE∽△DCB,
∴BC:CE=CD:BC,
∴BC2=CECD,
∴BC2=CE(CE+DE),
∴BC2=CE2+CEDE,
∴BC2- CE2= CEDE;
(3)如图,连接OC,
∵![]() ,AB是直径,
,AB是直径,
∴∠AOC=∠BOC=90°,
∴CE=OE+CO, BC=OB+CO ,
∵OA=4 ,E 是半径 OA 的中点,
∴BC=4![]() ,CE=2
,CE=2![]() ,
,
由(2)中 BC-CE=CE·DE,所以 DE=(BC-CE)÷CE=12÷2![]() =
= ![]() ,
,
故 DE=![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】在□ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的抛物线是二次函数![]() (a≠0)的图象,则下列结论:①abc>0;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b;⑤3a+c<0.其中正确的结论有
(a≠0)的图象,则下列结论:①abc>0;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b;⑤3a+c<0.其中正确的结论有
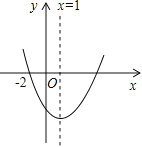
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
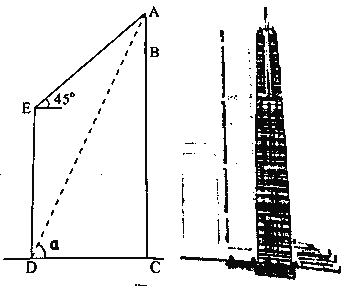
【题目】如图,长沙九龙仓国际金融中心主楼![]() 高达
高达![]() ,是目前湖南省第一高楼,和它处于同一水平面上的第二高楼
,是目前湖南省第一高楼,和它处于同一水平面上的第二高楼![]() 高
高![]() ,为了测量高楼
,为了测量高楼![]() 上发射塔
上发射塔![]() 的高度,在楼
的高度,在楼![]() 底端
底端![]() 点测得
点测得![]() 的仰角为α,
的仰角为α,![]() ,在顶端E测得A的仰角为
,在顶端E测得A的仰角为![]() ,求发射塔
,求发射塔![]() 的高度.
的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值 (单位:克) |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若标准质量为450克,则抽样检测的20袋食品的总质量为多少克?
(3)若该种食品的合格标准为450±5克,求该食品的抽样检测的合格率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:
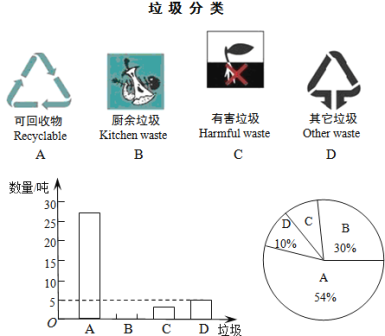
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在扇形统计图样中,产生的有害垃圾C所对应的圆心角 度;
(3)调查发现,在可回收物中塑料类垃圾占13%,每回收1吨塑料类垃圾可获得0.5吨二级原料.假设该城市每月产生的生活垃圾为1000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1) xx 2y 2 xy yx2 x2 y x 2y ;
(2) 已知:![]() ,求
,求![]() 和
和![]() 的值。
的值。
(3)化简并求值:(2a+b)2﹣(2a﹣b)(a+b)﹣2(a﹣2b)(a+2b),其中a=![]() ,b=-2.
,b=-2.
(4)已知![]() 求
求![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com