
【题目】如图,已知AB是⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.
(1)求证:∠PCA=∠ABC.
(2)过点A作AE∥PC交⊙O于点E,交CD于点F,连接BE,若cos∠P=![]() ,CF=10,求BE的长
,CF=10,求BE的长

【答案】(1)证明见解析;(2)BE=24.
【解析】(1)连接半径OC,根据切线的性质得:OC⊥PC,由圆周角定理得:∠ACB=90°,所以∠PCA=∠OCB,再由同圆的半径相等可得:∠OCB=∠ABC,从而得结论;
(2)先证明∠CAF=∠ACF,则AF=CF=10,根据cos∠P=cos∠FAD=![]() ,可得AD=8,FD=6,得CD=CF+FD=16,设OC=r,OD=r﹣8,根据勾股定理列方程可得r的值,再由三角函数cos∠EAB=
,可得AD=8,FD=6,得CD=CF+FD=16,设OC=r,OD=r﹣8,根据勾股定理列方程可得r的值,再由三角函数cos∠EAB=![]() ,可得AE的长,从而计算BE的长.
,可得AE的长,从而计算BE的长.
详解:证明:(1)连接OC,交AE于H,

∵PC是⊙O的切线,
∴OC⊥PC,
∴∠PCO=90°,
∴∠PCA+∠ACO=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACO+∠OCB=90°,
∴∠PCA=∠OCB,
∵OC=OB,
∴∠OCB=∠ABC,
∴∠PCA=∠ABC;
(2)∵AE∥PC,
∴∠CAF=∠PCA,
∵AB⊥CG,
∴![]() ,
,
∴∠ACF=∠ABC,
∵∠ABC=∠PCA,
∴∠CAF=∠ACF,
∴AF=CF=10,
∵AE∥PC,
∴∠P=∠FAD,
∴cos∠P=cos∠FAD=![]() ,
,
在Rt△AFD中,cos∠FAD=![]() ,AF=10,
,AF=10,
∴AD=8,
∴FD=![]() =6,
=6,
∴CD=CF+FD=16,
在Rt△OCD中,设OC=r,OD=r﹣8,
r2=(r﹣8)2+162,
r=20,
∴AB=2r=40,
∵AB是直径,
∴∠AEB=90°,
在Rt△AEB中,cos∠EAB=![]() ,AB=40,
,AB=40,
∴AE=32,
∴BE=![]() =24.
=24.


科目:初中数学 来源: 题型:
【题目】(2017四川省凉山州,第24题,8分)为了推进我州校园篮球运动的发展,2017年四川省中小学生男子篮球赛于2月在西昌成功举办.在此期间,某体育文化用品商店计划一次性购进篮球和排球共60个,其进价与售价间的关系如下表:

(1)商店用4200元购进这批篮球和排球,求购进篮球和排球各多少个?
(2)设商店所获利润为y(单位:元),购进篮球的个数为x(单位:个),请写出y与x之间的函数关系式(不要求写出x的取值范围);
(3)若要使商店的进货成本在4300元的限额内,且全部销售完后所获利润不低于1400元,请你列举出商店所有进货方案,并求出最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知P(1,2).
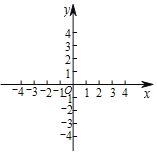
(1)在平面直角坐标系中描出点P(保留画图痕迹);
(2)如果将点P向左平移3个单位长度,再向上平移1个单位长度得到点P',则点P'的坐标为 .
(3)点A在坐标轴上,若S△OAP=2,直接写出满足条件的点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A,B两点,分别表示﹣40,20,甲、乙两只蚂蚁分别从A,B两点同时出发,甲沿线段AB方向以3个单位长度/秒的速度向右运动,甲到达点B处时运动停止;乙沿线段BA方向以5个单位长度/秒的速度向左运动.
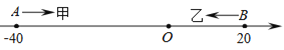
(1)求甲、乙第一次相遇点所表示的数.
(2)求经过多少秒时,甲、乙相距28个单位长度?
(3)若乙到达A点后立刻掉头追赶甲(速度保持不变),则在甲到达B点前,甲、乙是否还能再次相遇?若能,求出相遇点所表示的数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC.
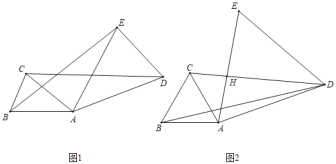
(1)如图1,在△ADE中,若AD=AE,且∠DAE=∠BAC,求证:CD=BE;
(2)如图2,在△ADE中,若∠DAE=∠BAC=60°,且CD垂直平分AE,AD=6,CD=8,求BD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家计划平均每天销售滑板车100辆,但实际的销售量与计划量有出入,下表是某周的销售情况(超额记为正,不足记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划数的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知该商家前三天共销售滑板车______辆;(直接写答案)
(2)根据记录的数据可知销售量最多的一天比销售量最少的-天多销售多少辆?
(3)本周实际销售量是多少?
(4)该商家实行每周计件工资制,每销售一辆车可得40元,若超额完成任务,则超过部分每辆另奖20元,少销售一辆扣25元,那么该商家的销售人员这一周的工资总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
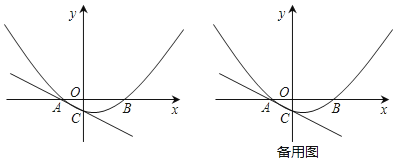
【题目】如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣![]() x﹣1交于点C.
x﹣1交于点C.
(1)求抛物线解析式及对称轴;
(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO的周长最小?若存在,求出点P的坐标,若不存在,请说明理由;
(3)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD.理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(______________________ ),
∴∠2 =∠CGD(等量代换).
∴CE∥BF(___________________________).
∴∠ =∠C(__________________________).
又∵∠B =∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD(________________________________).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com