
【题目】已知△ABC中,AB=AC.
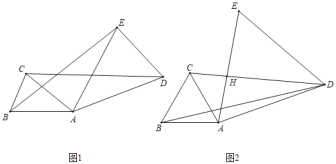
(1)如图1,在△ADE中,若AD=AE,且∠DAE=∠BAC,求证:CD=BE;
(2)如图2,在△ADE中,若∠DAE=∠BAC=60°,且CD垂直平分AE,AD=6,CD=8,求BD的长
【答案】(1)详见解析;(2)BD=10.
【解析】
(1)根据SAS证明△BAE和△CAD全等,再利用全等三角形的性质证明即可;
(2)根据等边三角形的性质和含30°的直角三角形的性质解答即可.
解:(1)∵∠DAE=∠BAC,
∴∠BAE=∠CAD,
在△BAE和△CAD中,
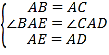 ,
,
∴△BAE≌△CAD(SAS),
∴CD=BE;
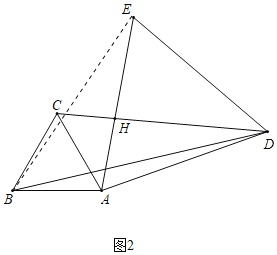
(2)解:连接BE,如图2所示:
∵AD=AE,∠DAE=60°,
∴△ADE是等边三角形,
∵CD垂直平分AE,
∴∠CDA=![]() ∠ADE=
∠ADE=![]() ×60°=30°,
×60°=30°,
∵△BAE≌△CAD,
∴BE=CD=8,∠BEA=∠CDA=30°,
∴BE⊥DE,
DE=AD=6,
∴BD=![]() =10.
=10.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
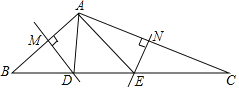
(1)若BC=8,则△ADE周长是多少?
(2)若∠BAC=118°,则∠DAE的度数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知长方形ABCD中,∠A=∠D=∠B=∠C=90,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm.

(1)求证:AF=DE.
(2)若AD+DC=18,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为( )
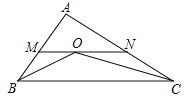
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.
(1)求证:∠PCA=∠ABC.
(2)过点A作AE∥PC交⊙O于点E,交CD于点F,连接BE,若cos∠P=![]() ,CF=10,求BE的长
,CF=10,求BE的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个四位数![]() ,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称
,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称![]() 为“幸运数”;如果一个正整数
为“幸运数”;如果一个正整数![]() 是另一个正整数
是另一个正整数![]() 的平方,则称正整数
的平方,则称正整数![]() 是完全平方数.若四位数
是完全平方数.若四位数![]() 为“幸运数”,且
为“幸运数”,且![]() 的三十三分之一是完全平方数,则符合条件的最大一个
的三十三分之一是完全平方数,则符合条件的最大一个![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校要开展校园文化艺术节活动,为了合理编排节目,对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次随机抽样调查(每名学生必须选择且只能选择一类),并将调查结果绘制成如下不完整统计图.
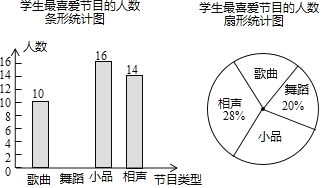
请你根据图中信息,回答下列问题:
(1)本次共调查了 名学生.
(2)在扇形统计图中,“歌曲”所在扇形的圆心角等于 度.
(3)补全条形统计图(标注频数).
(4)根据以上统计分析,估计该校2000名学生中最喜爱小品的人数为 人.
(5)九年一班和九年二班各有2名学生擅长舞蹈,学校准备从这4名学生中随机抽取2名学生参加舞蹈节目的编排,那么抽取的2名学生恰好来自同一个班级的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年三班的小雨同学想了解本校九年级学生对哪门课程感兴趣,随机抽取了部分九年级学生进行调查(每名学生必只能选择一门课程).将获得的数据整理绘制如下两幅不完整的统计图.
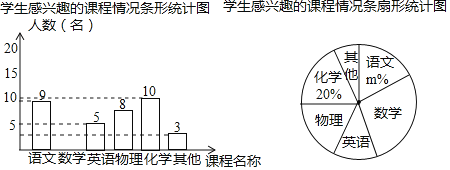
据统计图提供的信息,解答下列问题:
(1)在这次调查中一共抽取了 名学生,m的值是 .
(2)请根据据以上信息直在答题卡上补全条形统计图;
(3)扇形统计图中,“数学”所对应的圆心角度数是 度;
(4)若该校九年级共有1000名学生,根据抽样调查的结果,请你估计该校九年级学生中有多少名学生对数学感兴趣.
查看答案和解析>>
科目:初中数学 来源: 题型:
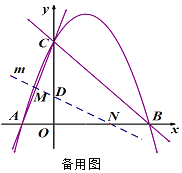
【题目】直线![]() 与x轴、y轴分别交于点B、C,抛物线
与x轴、y轴分别交于点B、C,抛物线![]() 经过点B、C,并与x轴交于另一点A.
经过点B、C,并与x轴交于另一点A.
(1)求此抛物线及直线AC的函数表达式;
(2)垂直于y轴的直线l与抛物线交于点P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() ),与直线BC交于点,N(
),与直线BC交于点,N(![]() ,
,![]() ),若
),若![]() <
<![]() <
<![]() ,结合函数的图象,求
,结合函数的图象,求![]() 的取值范围;
的取值范围;
(3)经过点D(0,1)的直线m与射线AC、射线OB分别交于点M、N.当直线m绕点D旋转时,![]() 是否为定值,若是,求出这个值,若不是,说明理由.
是否为定值,若是,求出这个值,若不是,说明理由.
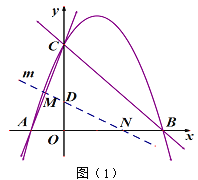
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com