
【题目】直线![]() 与x轴、y轴分别交于点B、C,抛物线
与x轴、y轴分别交于点B、C,抛物线![]() 经过点B、C,并与x轴交于另一点A.
经过点B、C,并与x轴交于另一点A.
(1)求此抛物线及直线AC的函数表达式;
(2)垂直于y轴的直线l与抛物线交于点P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() ),与直线BC交于点,N(
),与直线BC交于点,N(![]() ,
,![]() ),若
),若![]() <
<![]() <
<![]() ,结合函数的图象,求
,结合函数的图象,求![]() 的取值范围;
的取值范围;
(3)经过点D(0,1)的直线m与射线AC、射线OB分别交于点M、N.当直线m绕点D旋转时,![]() 是否为定值,若是,求出这个值,若不是,说明理由.
是否为定值,若是,求出这个值,若不是,说明理由.
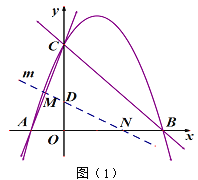
【答案】(1)=![]() ;
; ![]() ;(2)1<
;(2)1<![]() <2;(3)
<2;(3)![]() 为定值3.
为定值3.
【解析】(1)先求得直线y=-x+3与x轴、y轴的交点B、C的坐标,代入入![]() 求得a、k的值,即可得抛物线的函数表达式;令y=0,求得点A的坐标,再用待定系数法求得直线AC的函数表达式即可;(2)根据题意可得y1=y2,即可得x1+x2=2;当直线l1经过点C时,x1=x3=0,x2=2,此时x1+x3+x2=2,当直线l2经过顶点(1,4)时,直线BC的解析式为
求得a、k的值,即可得抛物线的函数表达式;令y=0,求得点A的坐标,再用待定系数法求得直线AC的函数表达式即可;(2)根据题意可得y1=y2,即可得x1+x2=2;当直线l1经过点C时,x1=x3=0,x2=2,此时x1+x3+x2=2,当直线l2经过顶点(1,4)时,直线BC的解析式为![]() ,y=4时,x=﹣1, 此时,x1=x2=1,x3=﹣1,此时x1+x3+x2=1;当直线l在直线l1与直线l2之间时,x3<x1<x2,即可得1<
,y=4时,x=﹣1, 此时,x1=x2=1,x3=﹣1,此时x1+x3+x2=1;当直线l在直线l1与直线l2之间时,x3<x1<x2,即可得1<![]() <2;(3)
<2;(3)![]() 为定值3,设直线MN的解析式为y=kx+1.把y=0代入y=kx+1得:kx+1=0,解得:x=
为定值3,设直线MN的解析式为y=kx+1.把y=0代入y=kx+1得:kx+1=0,解得:x=![]() ,所以点N的坐标为(
,所以点N的坐标为(![]() ,0).所以AN=
,0).所以AN=![]() +1=
+1=![]() 即可得
即可得![]() =
=![]() ;将y=3x+3与y=kx+1联立解得:x=
;将y=3x+3与y=kx+1联立解得:x=![]() .求得点M的横坐标为
.求得点M的横坐标为![]() . 过点M作MG⊥x轴,垂足为G.则AG=
. 过点M作MG⊥x轴,垂足为G.则AG=![]() =
=![]() .再由△MAG∽△CAO,根据相似三角形的性质可得
.再由△MAG∽△CAO,根据相似三角形的性质可得![]() ,
,![]() ,
,![]() =
=![]() =
=![]() ,由此可得
,由此可得![]() =
=![]() +
+![]() =
=![]() =3.
=3.
(1)∵直线y=-x+3与x轴、y轴分别交于点B、C,
∴B(3,0),C(0,3);
把B(3,0),C(0,3)代入![]() 得,
得,
![]() ,
,
解得![]() ,
,
∴抛物线函数表达式为![]() =
=![]() ;
;
令y=0,可得![]() =0,解得x1=-1,x2=3;
=0,解得x1=-1,x2=3;
∴A(-1,0);
设AC的解析式为y=kx+b,
![]() ,
,
解得![]() ,
,
∴直线AC的函数表达式为![]() ;
;
(2)∵y1=y2,∴x1+x2=2.
当直线l1经过点C时,x1=x3=0,x2=2,此时x1+x3+x2=2,
当直线l2经过顶点(1,4)时,直线BC的解析式为![]() ,y=4时,x=﹣1, 此时,x1=x2=1,x3=﹣1,此时x1+x3+x2=1;当直线l在直线l1与直线l2之间时,x3<x1<x2 ,
,y=4时,x=﹣1, 此时,x1=x2=1,x3=﹣1,此时x1+x3+x2=1;当直线l在直线l1与直线l2之间时,x3<x1<x2 ,
∴1<![]() <2.
<2.
(3)![]() 为定值3.
为定值3.
理由如下:设直线MN的解析式为y=kx+1.把y=0代入y=kx+1得:kx+1=0,解得:x=![]() ,
,
∴点N的坐标为(![]() ,0).∴AN=
,0).∴AN=![]() +1=
+1=![]() ,
,![]() =
=![]() ;
;
将y=3x+3与y=kx+1联立解得:x=![]() .∴点M的横坐标为
.∴点M的横坐标为![]() .
.
过点M作MG⊥x轴,垂足为G.则AG=![]() =
=![]() .
.
∵△MAG∽△CAO,∴![]() ,
,
∴![]() ,
,![]() =
=![]() =
=![]()
∴![]() =
=![]() +
+![]() =
=![]() =3.
=3.


科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC.
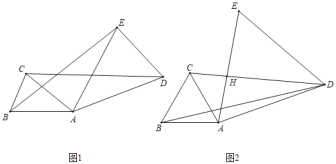
(1)如图1,在△ADE中,若AD=AE,且∠DAE=∠BAC,求证:CD=BE;
(2)如图2,在△ADE中,若∠DAE=∠BAC=60°,且CD垂直平分AE,AD=6,CD=8,求BD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查,过程如下,请补充完整.
(1)收集数据
从甲、乙两个班各随机抽取10名学生进行身体素质测试,测试成绩(百分制)如下:
甲班65 75 75 80 60 50 75 90 85 65
乙班90 55 80 70 55 70 95 80 65 70
(2)整理描述数据
按如下分数段整理、描述这两组样本数据:

在表中:m= ,n= .
(3)分析数据
①两组样本数据的平均数、中位数、众数如表所示:

在表中:x= ,y= .
②若规定测试成绩在80分(含80分)以上的叙述身体素质为优秀,请估计乙班50名学生中身体素质为优秀的学生有 人.
③现从甲班指定的2名学生(1男1女),乙班指定的3名学生(2男1女)中分别抽取1名学生去参加上级部门组织的身体素质测试,用树状图和列表法求抽到的2名同学是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师元旦节期间到武商众圆商场购买一台某品牌笔记本电脑,恰逢商场正推出“迎元旦”促销打折活动,具体优惠情况如表:
购物总金额(原价) | 折扣 |
不超过5000元的部分 | 九折 |
超过5000元且不超过10000元的部分 | 八折 |
超过10000元且不超过20000元的部分 | 七折 |
…… | …… |
例如:若购买的商品原价为15000元,实际付款金额为:
5000×90%+(10000﹣5000)×80%+(15000﹣10000)×70%=12000元.
(1)若这种品牌电脑的原价为8000元/台,请求出张老师实际付款金额;
(2)已知张老师购买一台该品牌电脑实际付费5700元.
①求该品牌电脑的原价是多少元/台?
②若售出这台电脑商场仍可获利14%,求这种品牌电脑的进价为多少元/台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD.理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(______________________ ),
∴∠2 =∠CGD(等量代换).
∴CE∥BF(___________________________).
∴∠ =∠C(__________________________).
又∵∠B =∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD(________________________________).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理a2+b2=c2本身就是一个关于a,b,c的方程,满足这个方程的正整数解(a,b,c)通常叫做勾股数组.毕达哥拉斯学派提出了一个构造勾股数组的公式,根据该公式可以构造出如下勾股数组:(3,4,5),(5,12,13),(7,24,25),….分析上面勾股数组可以发现,4=1×(3+1),12=2×(5+1),24=3×(7+1),…分析上面规律,第5个勾股数组为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
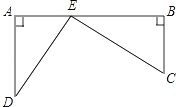
【题目】如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等.问:
(1)在离A站多少km处?
(2)判定三角形DEC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D、E.
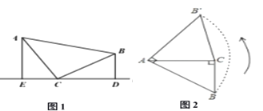
求证:△AEC≌△CDB;
(2)类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=6,将斜边AB绕点A逆时针旋转90°至AB,连接B,C,求△AB,C的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中秋节临近,某商场决定开展“金秋十月,回馈顾客”的让利活动,对部分品牌月饼进行打折销售,其中甲品牌月饼打八折,乙品牌月饼打七五折.已知打折前,买![]() 盒甲品牌月饼和
盒甲品牌月饼和![]() 盒乙品牌月饼需
盒乙品牌月饼需![]() 元;打折后,买
元;打折后,买![]() 盒甲品牌月饼和
盒甲品牌月饼和![]() 盒乙品牌月饼需
盒乙品牌月饼需![]() 元.
元.
(1)打折前甲、乙两种品牌月饼每盒分别为多少元?
(2)幸福敬老院需购买甲品牌月饼![]() 盒,乙品牌月饼
盒,乙品牌月饼![]() 盒,问打折后购买这批月饼比不打折节省了多少钱?
盒,问打折后购买这批月饼比不打折节省了多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com