
【题目】如图,在平面直角坐标系xOy中,已知P(1,2).
(1)在平面直角坐标系中描出点P(保留画图痕迹);
(2)如果将点P向左平移3个单位长度,再向上平移1个单位长度得到点P',则点P'的坐标为 .
(3)点A在坐标轴上,若S△OAP=2,直接写出满足条件的点A的坐标.
【答案】(1)点P的位置如图所示,见解析;(2)点P'的坐标为(﹣2,3);(3)点A的坐标为(0,4)或(0,﹣4)或(2,0)或(﹣2,0).
【解析】
(1)根据题意画出点P即可;
(2)根据平移的性质得出坐标即可;
(3)根据三角形的面积公式解答即可.
(1)点P的位置如图所示,
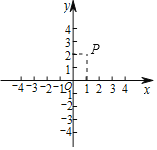
(2)将点P向左平移3个单位长度,再向上平移1个单位长度得到点P',则点P'的坐标为(﹣2,3),
故填:(﹣2,3);
(3)∵点A在坐标轴上,S△OAP=2,
当点A在x轴上时,△OAP的高为2,故OA的长为2,∴(2,0)或(﹣2,0).
当点A在y轴上时,△OAP的高为1,故OA的长为4,∴(0,4)或(0,﹣4).
∴点A的坐标为(0,4)或(0,﹣4)或(2,0)或(﹣2,0).


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图所示放置,使得一直角边重合,连接BD,CE.
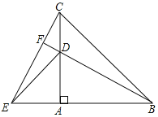
(1)求证:BD=CE;(2)延长BD,交CE于点F,求∠BFC的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过m(30<m≤100)人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队,收取总费用为y元.
(1)求y关于x的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
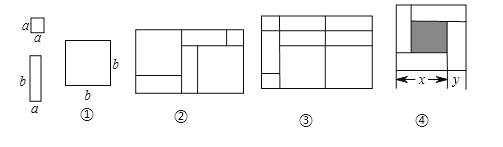
【题目】一天,小明和小玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式,比如图②可以解释为:![]()
(1)图③可以解释为等式: .
(2)要拼出一个长为a+3b,宽为2a+b的长方形,需要如图所示![]() 块,
块,![]() 块,
块,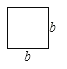 块.
块.
(3)如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个小长方形的两边长(x>y),观察图案,以下关系式正确的是 (填序号).
①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
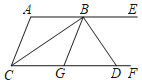
【题目】如图,AE∥CF,∠ACF的平分线交AE于点B,G是CF上的一点,∠GBE的平分线交CF于点D,且BD⊥BC,下列结论:①BC平分∠ABG;②AC∥BG;③与∠DBE互余的角有2个;④若∠A=α,则∠BDF=![]() .其中正确的有_____.(把你认为正确结论的序号都填上)
.其中正确的有_____.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知长方形ABCD中,∠A=∠D=∠B=∠C=90,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm.

(1)求证:AF=DE.
(2)若AD+DC=18,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,用字母表示的代数式是具有一般意义的.下列赋予3a实际意义的例子中不正确的是( )
A.若a表示一个等边三角形的边长,则3a表示这个等边三角形的周长
B.若苹果的价格是3元/千克,则3a表示买a千克苹果的金额
C.若一个两位数的十位数字是3和个位数字是a,则3a表示这个两位数
D.若一个圆柱体的底面积是3,高是a,则3a表示这个圆柱体的体积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.
(1)求证:∠PCA=∠ABC.
(2)过点A作AE∥PC交⊙O于点E,交CD于点F,连接BE,若cos∠P=![]() ,CF=10,求BE的长
,CF=10,求BE的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆形木材的直径是多少?”
如图所示,请根据所学知识计算:圆形木材的直径AC是( )
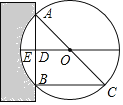
A. 13寸 B. 20寸 C. 26寸 D. 28寸
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com