Question

【题目】以点A为顶点作两个等腰直角三角形(△ABC，△ADE)，如图所示放置，使得一直角边重合，连接BD，CE．

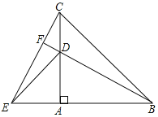
（1）求证：BD=CE；（2）延长BD，交CE于点F，求∠BFC的度数；

Answer 1

【答案】（1）详见解析；（2）90°.

【解析】

（1）根据等腰直角三角形的性质得到AB=AC，∠BAD=∠EAC=90°，AD=AE，利用“SAS”可证明△ADB≌△AEC，则BD=CE；

（2）由△ADB≌△AEC得到∠ACE=∠DBA，利用三角形内角和定理可得到∠BFC=180°-∠ACE-∠CDF=180°-∠DBA-∠BDA=∠DAB=90°；

(1)∵△ABC、△ADE是等腰直角三角形，

∴AB=AC,∠BAD=∠EAC=90°，AD=AE，

∵在△ADB和△AEC中，

，

∴△ADB≌△AEC(SAS)，

∴BD=CE；

(2)∵△ADB≌△AEC，

∴∠ACE=∠ABD，

而在△CDF中,∠BFC=180°∠ACE∠CDF

又∵∠CDF=∠BDA

∴∠BFC=180°∠DBA∠BDA=∠DAB=90°；