
����Ŀ��2019���й������ҵ�������ң�Ϊ��ռ���г�Ӯ��������������ij��ݹ�˾��̨�����ڿ���շѱ��������������ڵĿ��ͳһ��ȡ��������8Ԫ���������������10kg�������շ��ã������������10kg����10g�IJ��ְ�0.3Ԫ/kg�շѣ�
��1��ijͬѧ��Ҫ������Ϊx��x��10��ǧ�˵��鼮����������ͬ�ǿ�ݻؼң����ͬѧ�踶��ݷ���yԪ���ú�x�Ĵ���ʽ��ʾy��
��2��������ı���Ҫ��һЩ����Ʒ������������1800ǧ�ı������ÿ�ݹ�˾�����������������������շѱ����շѱ����±�����֪����Ʒ����Ϊaǧ�ˣ������Ʒ���������������Ŀ�ݷ�Ϊ����Ԫ�����ú�a�Ĵ���ʽ��ʾw��
�۸�� | |
������ | ����� |
������10kgͳһ��ȡ5Ԫ | 0.01Ԫ/km |
����10kg������50kg�IJ���0.2Ԫ/kg | |
����50kg����0.4Ԫ/kg | |
��ע����ݷѣ�������+����ѣ� | |
���𰸡���1��y=0.3x+5����2��w=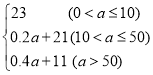 Ԫ.
Ԫ.
��������
��1�����ݡ��ܷ���=������+�����ѡ���ʽ���㼴�ɣ�
��2���������������0��a��10ʱ����10��a��50ʱ����a��50ʱ.���ݡ���ݷ�=������+����ѡ���ʽ����.
��1��y=8+0.3��(x��10)=0.3x+5��
��2����0��a��10��w=5+1800��0.01=23Ԫ��
��10��a��50��w=5+0.2(a��10)+1800��0.01=(0.2a+21)Ԫ��
��a��50ʱ��w=5+40��0.2+0.4��(a��50)+1800��0.01=(0.4a+11)Ԫ.
����������w=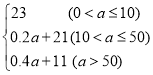 .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ԥ��ij���ϻᳩ��������1800Ԫ����һ���������ϣ����к��Ȼ����Ӧ������8100Ԫ�����������ϣ��ڶ������ϵ������ǵ�һ����3���������۱ȵ�һ����2Ԫ��
��1����һ�����Ͻ������۶���Ԫ��
��2�������ν����϶���ͬһ�۸����ۣ�����ȫ���������������2700Ԫ����ô���۵�������Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy����ֱ��y=2x+l��˫����y=![]() ��һ������ΪA��m��-3����
��һ������ΪA��m��-3����
��1����˫���ߵı���ʽ��
��2��������P��n��0����n��0���Ҵ�ֱ��x���ֱ����ֱ��y=2x+l��˫����y=![]() �Ľ���ֱ�ΪB��C������Bλ�ڵ�C�Ϸ�ʱ��ֱ��д��n��ȡֵ��Χ��
�Ľ���ֱ�ΪB��C������Bλ�ڵ�C�Ϸ�ʱ��ֱ��д��n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̶�м�2017��ɹ�����ȫ����������֮����������ȫ���������У�ijС��������Ӧ��������С���ڰ�װ�����������ܰ��ʾ�ƺ������䣬������2����ܰ��ʾ�ƺ�3�������乲��550Ԫ����������ĵ�������ܰ��ʾ�Ƶ��۵�3����
��1������ܰ��ʾ�ƺ�������ĵ��۸��Ƕ���Ԫ��
��2����С��������Ҫ����48�������䣬���������ܰ��ʾ�ƺ������乲100�����ҷ��ò�����10000Ԫ�������оٳ����й�������ָ�����ַ��������ʽ����٣������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ե�AΪ��������������ֱ��������(��ABC����ADE)����ͼ��ʾ���ã�ʹ��һֱ�DZ��غϣ�����BD��CE��
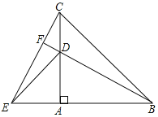
��1����֤��BD=CE����2���ӳ�BD����CE�ڵ�F�����BFC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��M��N��P��R�ֱ��������ϵ��ĸ���������Ӧ�ĵ㣬������һ������ԭ�㣬���ң�MN=NP=PR=1����a��Ӧ�ĵ���M��N֮�䣬��b��Ӧ�ĵ���P��R֮�䣬��|a|+|b|=2,��ԭ���ǣ���M��N��P��R�е�һ������_____________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ı���ABCD�У�AB��CD��AB=8��DC=4����M��N�ֱ�Ϊ��AB��DC���е㣬��P�ӵ�D��������ÿ��1����λ���ٶȴ�D��C�����˶��������C��ֹͣ�˶���ͬʱ��Q�ӵ�B��������ÿ��3����λ���ٶȴ�B��A�����˶��������A������ԭ·���أ���P�����C���Qͬʱֹͣ�˶������P��Q�˶���ʱ��Ϊt�룬���Ե�M��N��P��QΪ������ı���Ϊƽ���ı���ʱ��t��ֵΪ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�п쳵�Ӽ�����ʻ���ҵ�,һ���������ҵ�����ʻ����.���ȷ�������ʻ��ʱ��ΪxСʱ,����֮��ľ���Ϊyǧ��,ͼ�е����߱�ʾy��x֮��ĺ�����ϵ.������֮��ľ����״�Ϊ300ǧ��ʱ,����_____Сʱ��,����֮��ľ����ٴ�Ϊ300ǧ��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ��������
����һ�����һ���������ĸ�λ���ֵ��ڳ���λ����֮���������λ����֮�ͣ���������Ϊ���������������磺��1+2=3������123��������������ͬ����55��1315Ҳ��������������
���϶�������![]() ����λ��������������������x��2��x��x+2�ֱ���������İ�λ���֣�ʮλ���֣���λ���֣����磺135��468��Ϊ����������
����λ��������������������x��2��x��x+2�ֱ���������İ�λ���֣�ʮλ���֣���λ���֣����磺135��468��Ϊ����������
���⣺
��1����֪a����������������������������������b��b��0��ʹ10a+bΪһ����������������b����Сֵ��
��2����֪һ����λ����������![]() ��һ�������������ĺ��ܱ�3��������c��a+d��b=4��֤��
��һ�������������ĺ��ܱ�3��������c��a+d��b=4��֤��![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com