
【题目】某超市预测某饮料会畅销、先用1800元购进一批这种饮料,面市后果然供不应求,又用8100元购进这种饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若两次进饮料都按同一价格销售,两批全部售完后,获利不少于2700元,那么销售单价至少为多少元?
【答案】(1)4元/瓶.(2) 销售单价至少为7元/瓶.
【解析】
(1)设第一批饮料进货单价为x元/瓶,则第二批饮料进货单价为(x+2)元/瓶,根据数量=总价÷单价结合第二批购进饮料的数量是第一批的3倍,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)由数量=总价÷单价可得出第一、二批购进饮料的数量,设销售单价为y元/瓶,根据利润=销售单价×销售数量﹣进货总价结合获利不少于2700元,即可得出关于y的一元一次不等式,解之取其最小值即可得出结论.
(1)设第一批饮料进货单价为x元/瓶,则第二批饮料进货单价为(x+2)元/瓶,
依题意,得:![]() =3×
=3×![]() ,
,
解得:x=4,
经检验,x=4是原方程的解,且符合题意.
答:第一批饮料进货单价是4元/瓶;
(2)由(1)可知:第一批购进该种饮料450瓶,第二批购进该种饮料1350瓶.
设销售单价为y元/瓶,
依题意,得:(450+1350)y﹣1800﹣8100≥2700,
解得:y≥7.
答:销售单价至少为7元/瓶.


科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程满足方程组![]() .
.
(1)若x﹣y=2,求m的值;
(2)若x,y,m均为非负数,求m的取值范围,并化简式子|m﹣3|+|m﹣4|;
(3)在(2)的条件下求s=2x﹣3y+m的最小值及最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,∠BAO=30°,以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点D.
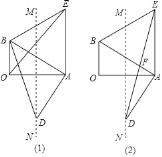
(1)连接BD,OE.求证:BD=OE;
(2)连接DE交AB于F.求证:F为DE的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
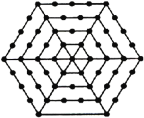
【题目】如图,有一个形如六边形的点阵,它的中心是一个点,作为第一层,第二层每边有两个点,第三层每边有三个点,依此类推.
(1)填写下表:
层 数 | 1 | 2 | 3 | 4 | 5 | … |
该层对应的点数 | 1 | 6 | … |
(2)写出第n层所对应的点数(n≥2).
(3)如果某一层共96个点,你知道它是第几层吗?
(4)有没有一层,它的点数为100个?
(5)写出n层的六边形点阵的总点数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形ABC的直角边AB=6,BC=8,将直角三角形ABC沿边BC的方向平移到三角形DEF的位置,DE交AC于点G,BE=2,三角形CEG的面积为13.5,下列结论:
①三角形ABC平移的距离是4; ②EG=4.5;
③AD∥CF; ④四边形ADFC的面积为6.
其中正确的结论是( )

A. ①② B. ②③ C. ③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为坐标原点,点A(1,5)和点B(m,1)均在反比例函数y= ![]() 图象上.
图象上.
(1)求m,k的值;
(2)设直线AB与x轴交于点C,求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】认真阅读并填空:
已知:如图,∠1=∠2,∠C=∠D,试说明:∠A=∠F.

解:∵∠1=∠2(已知),∠2=∠3( )
∴∠1=∠3(等量代换)
∴BD∥EC( )
∴∠4=∠C(两直线平行,同位角相等)
又∠C=∠D(已知)
∴∠4=∠D( )
∴ ∥ (内错角相等,两直线平行)
∴∠A=∠F( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区计划购进A、B两种树苗,已知1株A种树苗和2株B种树苗共20元,且A种树苗比B种树苗每株多2元.
(1)A、B两种树苗每株各多少元?
(2)若购买A、B两种树苗共360株,并且A种树苗的数量不少于B种树苗数量的一半,请你设计一种费用最省的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为一种新型电子产品在该城市的特约经销商,已知每件产品的进价为40元,该公司每年销售这种产品的其他开支(不含进货价)总计100万元,在销售过程中得知,年销售量y(万件)与销售单价x(元)之间存在如表所示的函数关系,并且发现y是x的一次函数.
销售单价x(元) | 50 | 60 | 70 | 80 |
销售数量y(万件) | 5.5 | 5 | 4.5 | 4 |
(1)求y与x的函数关系式;
(2)问:当销售单价x为何值时,该公司年利润最大?并求出这个最大值;
【备注:年利润=年销售额﹣总进货价﹣其他开支】
(3)若公司希望年利润不低于60万元,请你帮助该公司确定销售单价的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com