
【题目】某公司为一种新型电子产品在该城市的特约经销商,已知每件产品的进价为40元,该公司每年销售这种产品的其他开支(不含进货价)总计100万元,在销售过程中得知,年销售量y(万件)与销售单价x(元)之间存在如表所示的函数关系,并且发现y是x的一次函数.
销售单价x(元) | 50 | 60 | 70 | 80 |
销售数量y(万件) | 5.5 | 5 | 4.5 | 4 |
(1)求y与x的函数关系式;
(2)问:当销售单价x为何值时,该公司年利润最大?并求出这个最大值;
【备注:年利润=年销售额﹣总进货价﹣其他开支】
(3)若公司希望年利润不低于60万元,请你帮助该公司确定销售单价的范围.
【答案】
(1)解:设y=kx+b,把(60,5),(80,4)代入得: ![]() ,
,
解得: 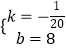 ,
,
故答案为:y=﹣ ![]() x+8;
x+8;
(2)解:该公司年利润w=(﹣ ![]() x+8)(x﹣40)﹣100=﹣
x+8)(x﹣40)﹣100=﹣ ![]() (x﹣100)2+80,
(x﹣100)2+80,
当x=100时,该公司年利润最大值为80万元;
(3)解:由题意得:﹣ ![]() (x﹣100)2+80=60,
(x﹣100)2+80=60,
解得:x1=80,x2=120,
故该公司确定销售单价x的范围是:80≤x≤120.
【解析】(1)利用表格,用待定系数法就可以求出y与x的函数关系式;
(2)该公司的年利润=年销售数量![]() 单件利润-公司每年销售这种产品的其他开支(不含进货价)总计100万元,列出函数关系式,并配成顶点式就可以得出结论;
单件利润-公司每年销售这种产品的其他开支(不含进货价)总计100万元,列出函数关系式,并配成顶点式就可以得出结论;
(3)根据公司希望年利润不低于60万元得出方程求解即可得出该公司确定销售单价的范围.
【考点精析】本题主要考查了二次函数的最值的相关知识点,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】某超市预测某饮料会畅销、先用1800元购进一批这种饮料,面市后果然供不应求,又用8100元购进这种饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若两次进饮料都按同一价格销售,两批全部售完后,获利不少于2700元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() +bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).
+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).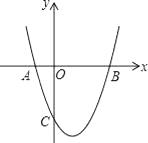
(1)求抛物线的解析式;
(2)D是y轴正半轴上的点,OD=3,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,
①试说明EF是圆的直径;
②判断△AEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(6,c)三点,其中a,b,c满足关系式|a-2|+(b-3)2+![]() =0,
=0,
(1)求A.B.C的坐标;
(2)求三角形ABC的面积;
(3)在y轴上是否存在点P,使三角形APC的面积与三角形ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=90°,∠BCD=135°,且AB=3cm,BC=7cm,CD=5![]() cm,点M从点A出发沿折线A﹣B﹣C﹣D运动到点D,且在AB上运动的速度为
cm,点M从点A出发沿折线A﹣B﹣C﹣D运动到点D,且在AB上运动的速度为![]() cm/s,在BC上运动的速度为1cm/s,在CD上运动的速度为
cm/s,在BC上运动的速度为1cm/s,在CD上运动的速度为![]() cm/s,连接AM、DM,当点M运动时间为_____(s)时,△ADM是直角三角形.
cm/s,连接AM、DM,当点M运动时间为_____(s)时,△ADM是直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
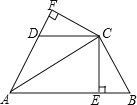
【题目】(本题8分) 已知,如图,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=DC.
(1)求证:BE=DF;
(2)若AB=5,AD=3,求AE的长;
(3)若△ABC的面积是23,△ADC面积是18,则△BEC的面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某种车的耗油量,我们对这种车在高速公路以100km/h的速度做了耗油试验,并把试验的数据记录下来,制成下表:
汽车行驶时间t(h) | 0 | 1 | 2 | 3 | … | |
油箱剩余油量Q(L) | 100 | 94 | 88 | 82 | … |
(1)根据上表的数据,你能用t表示Q吗?试一试;
(2)汽车行驶6h后,油箱中的剩余油量是多少?
(3)若汽车油箱中剩余油量为52L,则汽车行驶了多少小时?
(4)若该种汽车油箱只装了36L汽油,汽车以100km/h的速度在一条全长700公里的高速公路上匀速行驶,请问它在中途不加油的情况下能从高速公路起点开到高速公路终点吗,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是8×8的正方形网格,每个小方格都是边长为1的正方形,A、B是格点(网格线的交点).以网格线所在直线为坐标轴,在网格中建立平面直角坐标系xOy,使点A坐标为(﹣2,4).
(1)在网格中,画出这个平面直角坐标系;
(2)在第二象限内的格点上找到一点C,使A、B、C三点组成以AB为底边的等腰三角形,且腰长是无理数,则点C的坐标是 ;并画出△ABC关于y轴对称的△A′B′C′.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com