
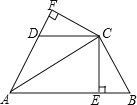
【题目】(本题8分) 已知,如图,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=DC.
(1)求证:BE=DF;
(2)若AB=5,AD=3,求AE的长;
(3)若△ABC的面积是23,△ADC面积是18,则△BEC的面积等于 .
【答案】(1)证明见解析;(2)4;(3)2.5.
【解析】试题分析:(1)根据HL证明Rt△BCE与Rt△DCF全等,再利用全等三角形的性质解答即可;
(2)根据全等三角形的性质解答即可;
(3)利用三角形的面积公式解答即可.
试题解析:解:(1)相等,∵AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,∴CE=CF,在Rt△BCE与Rt△DCF中,∵CE=CF,BC=CD,∴Rt△BCE≌Rt△DCF(HL),∴BE=DF;
(2)∵Rt△BCE≌Rt△DCF,∴DF=EB,CE=CF,CE⊥AB于E,CF⊥AD于F,在Rt△ACE与Rt△ACF中,∵CE=CF,AC=AC,∴Rt△ACERt△ACF(HL),∴AF=AE,∵DF=1,AD=3,∴AB=AF+BE=AD+DF+BE=5;
(3)∵Rt△BCE≌Rt△DCF,∵△ABC的面积是23,△ADC面积是18,∴△BEC的面积=![]() ×(23-18)=2.5.
×(23-18)=2.5.


科目:初中数学 来源: 题型:
【题目】对于四舍五入得到的近似数1.50万,下列说法中正确的是( )
A. 该近似数精确到百分位 B. 该近似数精确到十分位
C. 该近似数精确到千位 D. 该近似数精确到百位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用长为32米的篱笆围成一个矩形养鸡场,设围成的矩形一边长为x米,面积为y平方米.
(1)求y关于x的函数关系式;
(2)当x为何值时,围成的养鸡场面积为60平方米?
(3)能否围成面积最大的养鸡场?如果能,请求出其边长及最大面积;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MON=90°,有一根长为10的木棒AB的两个端点A、B分别在射线OM,ON上滑动,∠OAB的角平分线AD交OB于点D.
(1)如图(1),若OA=6,则OB= ,OD= ;
(2)如图(2),过点B作BE⊥AD,交AD的延长线于点E,连接OE,在AB滑动的过程中,线段OE,BE有何数量关系,并说明理由;
(3)若点P是∠MON内部一点,在(1)的条件下,当△ABP是以AB为斜边的等腰直角三角形时,OP2= ;
(4)在AB滑动的过程中,△AOB面积的最大值为 .



·图(1) 图(2) 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
(1)若EF=5,BC=12,求△EFM的周长;
(2)若∠ABC=50°,∠ACB=70°,求∠FME的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按图填空,并注明理由. 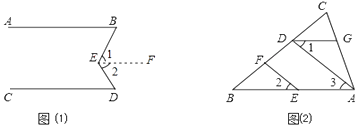
(1)完成正确的证明:如图(1),已知AB∥CD,求证:∠BED=∠B+∠D
证明:过E点作EF∥AB(经过直线外一点有且只有一条直线与这条直线平行)
∴∠1=()
∵AB∥CD(已知)
∴EF∥CD(如果两条直线与同一直线平行,那么它们也平行)
∴∠2=()
又∠BED=∠1+∠2
∴∠BED=∠B+∠D (等量代换).
(2)如图(2),在△ABC中,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解:因为EF∥AD(已知)
所以∠2=∠3.()
又因为∠1=∠2,所以∠1=∠3.(等量代换)
所以AB∥()
所以∠BAC+=180° ().
又因为∠BAC=70°,所以∠AGD=110°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
(1)请你补全这个输水管道的圆形截面;
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com