
����Ŀ����ͼ��8��8������������ÿ��С�����DZ߳�Ϊ1�������Σ�A��B�Ǹ�㣨�����ߵĽ��㣩��������������ֱ��Ϊ�����ᣬ�������н���ƽ��ֱ������ϵxOy��ʹ��A����Ϊ����2��4����
(1)�������У��������ƽ��ֱ������ϵ��
(2)�ڵڶ������ڵĸ�����ҵ�һ��C��ʹA��B��C���������ABΪ�ױߵĵ��������Σ��������������������C���������� ������������ABC����y��ԳƵġ�A��B��C�䣮

 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾Ϊһ�����͵��Ӳ�Ʒ�ڸó��е���Լ�����̣���֪ÿ����Ʒ�Ľ���Ϊ40Ԫ���ù�˾ÿ���������ֲ�Ʒ��������֧�����������ۣ��ܼ�100��Ԫ�������۹����е�֪����������y������������۵���x��Ԫ��֮����������ʾ�ĺ�����ϵ�����ҷ���y��x��һ�κ�����
���۵���x��Ԫ�� | 50 | 60 | 70 | 80 |
��������y������� | 5.5 | 5 | 4.5 | 4 |
��1����y��x�ĺ�����ϵʽ��
��2���ʣ������۵���xΪ��ֵʱ���ù�˾������������������ֵ��
����ע��������=�����۶�ܽ����۩�������֧��
��3������˾ϣ����������60��Ԫ����������ù�˾ȷ�����۵��۵ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=3��BC=5����BΪԲ��BCΪ�뾶������AD�ڵ�E������CE����BF��CE������ΪF����tan��FBC��ֵΪ�� ��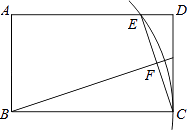
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������ĸ��������� ��BAC=��DCA���� ��DAC=��BCA���� ��ABD=��CDB���� ��ADB=��CBD��������ʹ AD��BC�������ǣ� ��

A.�٢�B.�ۢ�C.�ڢ�D.�٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ı���![]() �У�
��![]() ��
��![]() .
.
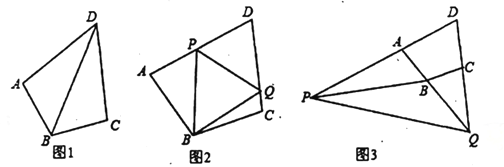
(1)��ͼ1������![]() ����
����![]() ����֤��
����֤��![]() .
.
(2)��ͼ2����![]() �ֱ����߶�
�ֱ����߶�![]() �ϣ�����
�ϣ�����![]() ����֤��
����֤��![]() ;
;
(3)����![]() ��
��![]() ���ӳ����ϣ���
���ӳ����ϣ���![]() ��
��![]() ���ӳ����ϣ���ͼ3��ʾ����Ȼ����
���ӳ����ϣ���ͼ3��ʾ����Ȼ����![]() ����д��
�����![]() ��
��![]() ��������ϵ��������֤�����̣�
��������ϵ��������֤�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�ABCD�DZ߳�Ϊ60cm��������ӲֽƬ����ȥ�ĸ�ȫ�ȵĵ���ֱ�������Σ���Ӱ������ʾ��������E��F��AB�ϣ������������𣬵�A��B��C��Dǡ���غ��ڵ�O������ͼ����ʾ�����γ���һ������Ϊ������GHMN�İ�װ�У���AE=x ��cm����
��1�����߶�GF�ij������ú�x�Ĵ���ʽ��ʾ��
��2����xΪ��ֵʱ������GHPF�����S ��cm2�����������Ϊ���٣�
��3�����ʣ����ְ�װ���ܷ����һ������뾶Ϊ15cm����Ϊ10cm��Բ���ι���Ʒ����ʹ��Բ���ι���Ʒ��һ������ǡ������ͼ���е�������GHMN�ڣ����ܣ����������������x��ֵ��Χ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶ij��ͬѧ����ף2015��Ԫ�������Ͻ��г齱�����һ�������Ŀڴ�����������ȫ��ͬ��С�����Ƿֱ���1��2��3���������һ��С����±�ź�Ż�ҡ�ȣ��ٴ����������һ��С����±�ţ�
��1�������б�������ͼ�ķ�����ֻѡ����һ�֣�����ʾ��������С���ϵı�ŵ����н����
��2���涨������������С������ͬʱ�н������н��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AB=AD��AC=5����DAB=��DCB=90�������ı���ABCD�����Ϊ��������

A. 15 B. 12.5 C. 14.5 D. 17
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪AB��CD����M��N�ֱ���AB��CD�����㣬��G��AB��CD֮�䣬����MG��NG��

��1����ͼ1����GM��GN�����AMG+��CNG�Ķ�����
��2����ͼ2������P��CD�·�һ�㣬MGƽ�֡�BMP��NDƽ�֡�GNP����֪��BMG��30�㣬���MGN+��MPN�Ķ�����
��3����ͼ3������E��AB�Ϸ�һ�㣬����EM��EN����GM���ӳ���MFƽ�֡�AME��NEƽ�֡�CNG��2��MEN+��MGN��105�㣬���AME�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com