
【题目】如图,已知△ABC中,CE⊥AB于E,BF⊥AC于F,在不添加字母的情况下,找出图中所有的相似三角形,并证明其中一组.
【答案】解:∵CE⊥AB于E,BF⊥AC于F,
∴∠AEC=∠AFB,
∵∠A=∠A,
∴△ABF∽△ACE;
∵CE⊥AB于E,BF⊥AC于F,
∴∠AEC=∠AFB=90°,
∴B、C、E、F四点在以BC为直径的圆上,
∴∠AFE=∠ABC,
∴△AEF∽△ACB.
【解析】根据垂线的定义得∠AEC=∠AFB,又∠A=∠A,根据两角对应相等得两个三角形相似得出△ABF∽△ACE;根据垂线的定义知∠AEC=∠AFB=90°从而得出B、C、E、F四点在以BC为直径的圆上根据圆内接四边形的一个外角等于它的内对角得出∠AFE=∠ABC,根据两角对应相等得两个三角形相似得出△AEF∽△ACB.
【考点精析】解答此题的关键在于理解圆内接四边形的性质的相关知识,掌握把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形,以及对相似三角形的判定的理解,了解相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).


科目:初中数学 来源: 题型:
【题目】如图,直角三角形ABC的直角边AB=6,BC=8,将直角三角形ABC沿边BC的方向平移到三角形DEF的位置,DE交AC于点G,BE=2,三角形CEG的面积为13.5,下列结论:
①三角形ABC平移的距离是4; ②EG=4.5;
③AD∥CF; ④四边形ADFC的面积为6.
其中正确的结论是( )

A. ①② B. ②③ C. ③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件:①∠A﹣∠B=∠C; ②∠A:∠B:∠C=2:3:5; ③∠A=![]() ∠B=
∠B= ![]() ∠ C;④∠A=∠B=2∠C;⑤∠A=∠B=
∠ C;④∠A=∠B=2∠C;⑤∠A=∠B= ![]() ∠C,其中能确定△ABC 为直角三角形的条件有 ( )
∠C,其中能确定△ABC 为直角三角形的条件有 ( )
A.2 个B.3 个C.4 个D.5 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为一种新型电子产品在该城市的特约经销商,已知每件产品的进价为40元,该公司每年销售这种产品的其他开支(不含进货价)总计100万元,在销售过程中得知,年销售量y(万件)与销售单价x(元)之间存在如表所示的函数关系,并且发现y是x的一次函数.
销售单价x(元) | 50 | 60 | 70 | 80 |
销售数量y(万件) | 5.5 | 5 | 4.5 | 4 |
(1)求y与x的函数关系式;
(2)问:当销售单价x为何值时,该公司年利润最大?并求出这个最大值;
【备注:年利润=年销售额﹣总进货价﹣其他开支】
(3)若公司希望年利润不低于60万元,请你帮助该公司确定销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于 ![]() 的一元二次方程m
的一元二次方程m ![]() +2x-1=0有两个不相等的实数根,则
+2x-1=0有两个不相等的实数根,则 ![]() 的取值范围是( )
的取值范围是( )
A.m<-1
B.m>1
C.m<1且m≠0
D.m>-1且m≠0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(x-2)(x-3)=m有实数根x1 , x2 , 且x1![]() x2有下列结论:
x2有下列结论:
①x1=2,x2=3;②m> ![]() ;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).
;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).
其中正确的结论是(填正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
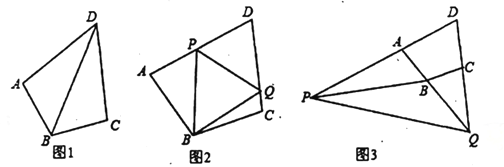
【题目】已知在四边形![]() 中,
中,![]() ,
,![]() .
.
(1)如图1.连接![]() ,若
,若![]() ,求证:
,求证:![]() .
.
(2)如图2,点![]() 分别在线段
分别在线段![]() 上,满足
上,满足![]() ,求证:
,求证:![]() ;
;
(3)若点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 的延长线上,如图3所示,仍然满足
的延长线上,如图3所示,仍然满足![]() ,请写出
,请写出![]() 与
与![]() 的数量关系,并给出证明过程.
的数量关系,并给出证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com