
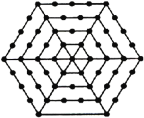
【题目】如图,有一个形如六边形的点阵,它的中心是一个点,作为第一层,第二层每边有两个点,第三层每边有三个点,依此类推.
(1)填写下表:
层 数 | 1 | 2 | 3 | 4 | 5 | … |
该层对应的点数 | 1 | 6 | … |
(2)写出第n层所对应的点数(n≥2).
(3)如果某一层共96个点,你知道它是第几层吗?
(4)有没有一层,它的点数为100个?
(5)写出n层的六边形点阵的总点数.
【答案】(1)12、18、24;(2)6(n-1)(n≥2);(3)17;(4)没有;(5)![]() .
.
【解析】
(1)根据题目中的图形和题意,可以将表格中的数据补充完整;
(2)根据(1)中填写的表格找规律即可得出答案;
(3)根据(2)中得出的第n层所对应的点数等于96,求出n即可得出答案;
(4)根据(2)中得出的第n层所对应的点数等于100,看求出的n是否为整数即可得出答案;
(5)根据(2)中得出的第n层所对应的点数,把每一层所对应的点数相加即可得出答案.
(1)填写下表:
层数 | 1 | 2 | 3 | 4 | 5 | … | |
该层对应的点数 | 1 | 6 | 12 | 18 | 24 | … |
(2)根据(1)中所填表格可发现规律,
第n层所对应点数为:6(n-1)(n≥2);
(3)6(n-1)=96,
n=17;
(4)6(n-1)=100,
n=![]() ,
,
所以没有一层,它的点数为100个;
(5)1+6×1+6×2+6×3+6×4+...+6×(n-1)
=1+6×(1+2+3+4+…+n-1)
=1+![]()
=![]() .
.


科目:初中数学 来源: 题型:
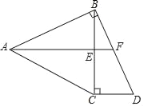
【题目】如图,在等腰△ABC中,AB=AC,过点B作BD⊥AB,过点C作CD⊥BC,两线相交于点D,AF平分∠BAC交BC于点E,交BD于点F.
(1)若∠BAC=68°,求∠DBC;
(2)求证:点F为BD中点;
(3)若AC=BD,且CD=3,求四边形ABDC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
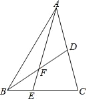
【题目】如图,△ABC中,点E是BC上的一点,EC=2BE,点D是AC的中点.若△ABC的面积S△ABC=12,则S△ADF﹣S△BEF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[知识生成]通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
例如:如图①是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
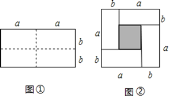
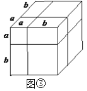
(1)图②中阴影部分的正方形的边长是________________;
(2)请用两种不同的方法求图②中阴影部分的面积:
方法1:________________________;方法2:_______________________;
(3)观察图②,请你写出(a+b)2、![]() 、
、![]() 之间的等量关系是____________________________________________;
之间的等量关系是____________________________________________;
(4)根据(3)中的等量关系解决如下问题:若![]() ,
,![]() ,则
,则![]() =
=
[知识迁移]
类似地,用两种不同的方法计算同一几何体的体积,也可以得到一个恒等式.
(5)根据图③,写出一个代数恒等式:____________________________;
(6)已知![]() ,
,![]() ,利用上面的规律求
,利用上面的规律求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点A、B表示的点分别为-6和3
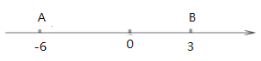
(1)若数轴上有一点P,它到A和点B的距离相等,则点P对应的数字是________(直接写出答案)
(2)在上问的情况下,动点Q从点P出发,以3个单位长度/秒的速度在数轴上向左移动,是否存在某一个时刻,Q点与B点的距离等于 Q点与A点的距离的2倍?若存在,求出点Q运动的时间,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
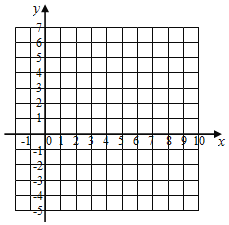
【题目】如图,在平面直角坐标系中,△ABC顶点的坐标分别是A(﹣1,3)、B(﹣5,1)、C(﹣2,﹣2).
(1)画出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′各顶点的坐标;
(2)求出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料会畅销、先用1800元购进一批这种饮料,面市后果然供不应求,又用8100元购进这种饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若两次进饮料都按同一价格销售,两批全部售完后,获利不少于2700元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并解决有关问题:
我们知道,|m|= .现在我们可以用这一结论来化简含有绝对值的代
.现在我们可以用这一结论来化简含有绝对值的代
数式,如化简代数式|m+1|+|m﹣2|时,可令 m+1=0 和 m﹣2=0,分别求得 m=﹣1,m=2(称﹣1,2 分别为|m+1|与|m﹣2|的零点值).在实数范围内, 零点值 m=﹣1 和 m=2 可将全体实数分成不重复且不遗漏的如下 3 种情况:
(1)m<﹣1;(2)﹣1≤m<2;(3)m≥2.从而化简代数式|m+1|+|m﹣2| 可分以下 3 种情况:
(1)当 m<﹣1 时,原式=﹣(m+1)﹣(m﹣2)=﹣2m+1;
(2)当﹣1≤m<2 时,原式=m+1﹣(m﹣2)=3;
(3)当 m≥2 时,原式=m+1+m﹣2=2m﹣1.
综上讨论,原式=
通过以上阅读,请你解决以下问题:
(1)分别求出|x﹣5|和|x﹣4|的零点值;
(2)化简代数式|x﹣5|+|x﹣4|;
(3)求代数式|x﹣5|+|x﹣4|的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(6,c)三点,其中a,b,c满足关系式|a-2|+(b-3)2+![]() =0,
=0,
(1)求A.B.C的坐标;
(2)求三角形ABC的面积;
(3)在y轴上是否存在点P,使三角形APC的面积与三角形ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com