
ЁОЬтФПЁП[жЊЪЖЩњГЩ]ЭЈГЃЃЌгУСНжжВЛЭЌЕФЗНЗЈМЦЫуЭЌвЛИіЭМаЮЕФУцЛ§ЃЌПЩвдЕУЕНвЛИіКуЕШЪНЃЎ
Р§ШчЃКШчЭМЂйЪЧвЛИіГЄЮЊ![]() ЃЌПэЮЊ
ЃЌПэЮЊ![]() ЕФГЄЗНаЮЃЌбиЭМжаащЯпгУМєЕЖОљЗжГЩЫФИіаЁГЄЗНаЮЃЌШЛКѓАДЭМЂкЕФаЮзДЦДГЩвЛИіе§ЗНаЮЃЎЧыНтД№ЯТСаЮЪЬтЃК
ЕФГЄЗНаЮЃЌбиЭМжаащЯпгУМєЕЖОљЗжГЩЫФИіаЁГЄЗНаЮЃЌШЛКѓАДЭМЂкЕФаЮзДЦДГЩвЛИіе§ЗНаЮЃЎЧыНтД№ЯТСаЮЪЬтЃК
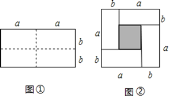
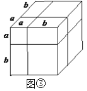
ЃЈ1ЃЉЭМЂкжавѕгАВПЗжЕФе§ЗНаЮЕФБпГЄЪЧ________________ЃЛ
ЃЈ2ЃЉЧыгУСНжжВЛЭЌЕФЗНЗЈЧѓЭМЂкжавѕгАВПЗжЕФУцЛ§ЃК
ЗНЗЈ1:________________________ЃЛЗНЗЈ2ЃК_______________________ЃЛ
ЃЈ3ЃЉЙлВьЭМЂкЃЌЧыФуаДГіЃЈa+bЃЉ2ЁЂ![]() ЁЂ
ЁЂ![]() жЎМфЕФЕШСПЙиЯЕЪЧ____________________________________________ЃЛ
жЎМфЕФЕШСПЙиЯЕЪЧ____________________________________________ЃЛ
ЃЈ4ЃЉИљОнЃЈ3ЃЉжаЕФЕШСПЙиЯЕНтОіШчЯТЮЪЬт:Шє![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() =
=
[жЊЪЖЧЈвЦ]
РрЫЦЕиЃЌгУСНжжВЛЭЌЕФЗНЗЈМЦЫуЭЌвЛМИКЮЬхЕФЬхЛ§ЃЌвВПЩвдЕУЕНвЛИіКуЕШЪНЃЎ
ЃЈ5ЃЉИљОнЭМЂлЃЌаДГівЛИіДњЪ§КуЕШЪНЃК____________________________ЃЛ
ЃЈ6ЃЉвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌРћгУЩЯУцЕФЙцТЩЧѓ
ЃЌРћгУЩЯУцЕФЙцТЩЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ a-bЃЛЃЈ2ЃЉ![]() ЃЛ
ЃЛ ![]() ЃЛ ЃЈ3ЃЉ
ЃЛ ЃЈ3ЃЉ![]() ЃЛЃЈ4ЃЉ 14ЃЛЃЈ5ЃЉ ЃЈa+bЃЉ3=a3+b3+3a2b+3ab2ЃЛЃЈ6ЃЉ 9ЃЎ
ЃЛЃЈ4ЃЉ 14ЃЛЃЈ5ЃЉ ЃЈa+bЃЉ3=a3+b3+3a2b+3ab2ЃЛЃЈ6ЃЉ 9ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЭМжБНгЧѓЕУБпГЄМДПЩЃЌ
ЃЈ2ЃЉвбжЊБпГЄжБНгЧѓУцЛ§ЃЌвѕгАУцЛ§ЪЧДѓе§ЗНаЮУцЛ§МѕШЅЫФИіГЄЗНаЮУцЛ§ЃЌПЩЕУД№АИЃЌ
ЃЈ3ЃЉРћгУУцЛ§ЯрЕШЭЦЕМЙЋЪН![]() ЃЛ
ЃЛ
ЃЈ4ЃЉРћгУЃЈ3ЃЉжаЕФЙЋЪНЧѓНтМДПЩЃЌ
ЃЈ5ЃЉРћгУЬхЛ§ЯрЕШЭЦЕМ![]() ЃЛ
ЃЛ
ЃЈ6ЃЉгІгУЃЈ5ЃЉжаЕФЙЋЪНМДПЩЃЎ
НтЃКЃЈ1ЃЉгЩЭМжБНгЧѓЕУвѕгАБпГЄЮЊa-bЃЛ
ЙЪД№АИЮЊЃКa-bЃЛ
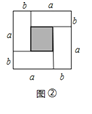
ЃЈ2ЃЉЗНЗЈвЛЃКвбжЊБпГЄжБНгЧѓУцЛ§ЮЊ![]() ЃЛ
ЃЛ
ЗНЗЈЖўЃКвѕгАУцЛ§ЪЧДѓе§ЗНаЮУцЛ§МѕШЅЫФИіГЄЗНаЮУцЛ§ЃЌ
ЁрУцЛ§ЮЊ![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊ![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉгЩвѕгАВПЗжУцЛ§ЯрЕШПЩЕУ![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊЃК ![]()
ЃЈ4ЃЉгЩ![]() ЃЌ
ЃЌ
ПЩЕУ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊ![]() ЃЛ
ЃЛ
ЃЈ5ЃЉЗНЗЈвЛЃКе§ЗНЬхРтГЄЮЊa+bЃЌ ЁрЬхЛ§ЮЊ![]() ЃЌ
ЃЌ
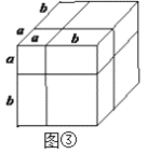
ЗНЗЈЖўЃКе§ЗНЬхЬхЛ§ЪЧГЄЗНЬхКЭаЁе§ЗНЬхЕФЬхЛ§КЭЃЌ
МД![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊ![]() ЃЛ
ЃЛ
ЃЈ6ЃЉЁп![]() ЃЛ
ЃЛ
НЋa+b=3ЃЌab=1ЃЌДњШыЕУЃК![]()
![]()
![]() ЃЛ
ЃЛ
![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
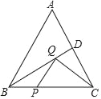
ЁОЬтФПЁПШчЭМЃЌЕШБпЁїABCЕФжмГЄЮЊ18cmЃЌBDЮЊACБпЩЯЕФжаЯпЃЌЖЏЕуPЃЌQЗжБ№дкЯпЖЮBCЃЌBDЩЯдЫЖЏЃЌСЌНгCQЃЌPQЃЌЕБBPГЄЮЊ_____cmЪБЃЌЯпЖЮCQ+PQЕФКЭЮЊзюаЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
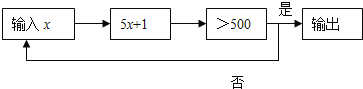
ЁОЬтФПЁПАДЯТУцГЬађМЦЫуЃЌМДИљОнЪфШыЕФ![]() ХаЖЯ
ХаЖЯ![]() ЪЧЗёДѓгк500ЃЌШєДѓгк500дђЪфГіЃЌНсЪјМЦЫуЃЌШєВЛДѓгк500ЃЌдђвдЯждкЕФ
ЪЧЗёДѓгк500ЃЌШєДѓгк500дђЪфГіЃЌНсЪјМЦЫуЃЌШєВЛДѓгк500ЃЌдђвдЯждкЕФ![]() ЕФжЕзїЮЊаТЕФ
ЕФжЕзїЮЊаТЕФ![]() ЕФжЕЃЌМЬајдЫЫуЃЌбЛЗЭљИДЃЌжБжСЪфГіНсЙћЮЊжЙЃЎШєПЊЪМЪфШы
ЕФжЕЃЌМЬајдЫЫуЃЌбЛЗЭљИДЃЌжБжСЪфГіНсЙћЮЊжЙЃЎШєПЊЪМЪфШы![]() ЕФжЕЮЊе§ећЪ§ЃЌзюКѓЪфГіЕФНсЙћЮЊ656ЃЌдђТњзуЬѕМўЕФЫљга
ЕФжЕЮЊе§ећЪ§ЃЌзюКѓЪфГіЕФНсЙћЮЊ656ЃЌдђТњзуЬѕМўЕФЫљга![]() ЕФжЕЪЧ__ЃЎ
ЕФжЕЪЧ__ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧЖўДЮКЏЪ§ ![]() ЭМЯѓЕФвЛВПЗжЃЌЖдГЦжсЮЊ
ЭМЯѓЕФвЛВПЗжЃЌЖдГЦжсЮЊ ![]() ЃЌЧвОЙ§ЕуЃЈ2ЃЌ0ЃЉЯТСаЫЕЗЈЃКЂйabc<0ЃЛЂк-2b+c=0ЃЛЂл4a+2b+c<0ЃЛЂмШє(-
ЃЌЧвОЙ§ЕуЃЈ2ЃЌ0ЃЉЯТСаЫЕЗЈЃКЂйabc<0ЃЛЂк-2b+c=0ЃЛЂл4a+2b+c<0ЃЛЂмШє(- ![]() ЃЌy1)ЃЌ(
ЃЌy1)ЃЌ( ![]() ЃЌy2)ЪЧХзЮяЯпЩЯЕФСНЕуЃЌдђy1<y2ЃЛЂн
ЃЌy2)ЪЧХзЮяЯпЩЯЕФСНЕуЃЌдђy1<y2ЃЛЂн ![]() >m(am+b)Цфжа(mЁй
>m(am+b)Цфжа(mЁй ![]() )ЦфжаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
)ЦфжаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ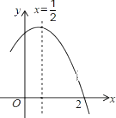
A.ЂйЂкЂмЂн
B.ЂлЂм
C.ЂйЂл
D.ЂйЂкЂн
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїAOBжаЃЌЁЯAOBЃН90ЁуЃЌЁЯBAOЃН30ЁуЃЌвдABЮЊвЛБпзїЕШБпЁїABEЃЌзїOAЕФДЙжБЦНЗжЯпMNНЛABЕФДЙЯпADгкЕуDЃЎ
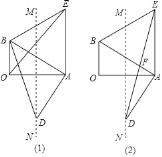
ЃЈ1ЃЉСЌНгBDЃЌOEЃЎЧѓжЄЃКBDЃНOEЃЛ
ЃЈ2ЃЉСЌНгDEНЛABгкFЃЎЧѓжЄЃКFЮЊDEЕФжаЕуЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЃК
ЃЈ1ЃЉ ![]() ЃЈ2ЃЉ
ЃЈ2ЃЉ ![]()
ЃЈ3ЃЉ 7.5+ЃЈЉ2![]() ЃЉЉЃЈ+22.5ЃЉ+ЃЈЉ6
ЃЉЉЃЈ+22.5ЃЉ+ЃЈЉ6![]() ЃЉ ЃЈ4ЃЉ
ЃЉ ЃЈ4ЃЉ ![]()
ЃЈ5ЃЉ 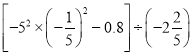 ЃЈ6ЃЉ
ЃЈ6ЃЉ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
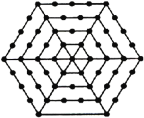
ЁОЬтФПЁПШчЭМЃЌгавЛИіаЮШчСљБпаЮЕФЕуеѓЃЌЫќЕФжааФЪЧвЛИіЕуЃЌзїЮЊЕквЛВуЃЌЕкЖўВуУПБпгаСНИіЕуЃЌЕкШ§ВуУПБпгаШ§ИіЕуЃЌвРДЫРрЭЦЃЎ
ЃЈ1ЃЉЬюаДЯТБэЃК
Ву Ъ§ | 1 | 2 | 3 | 4 | 5 | Ё |
ИУВуЖдгІЕФЕуЪ§ | 1 | 6 | Ё |
ЃЈ2ЃЉаДГіЕкnВуЫљЖдгІЕФЕуЪ§ЃЈnЁн2ЃЉЃЎ
ЃЈ3ЃЉШчЙћФГвЛВуЙВ96ИіЕуЃЌФужЊЕРЫќЪЧЕкМИВуТ№ЃП
ЃЈ4ЃЉгаУЛгавЛВуЃЌЫќЕФЕуЪ§ЮЊ100ИіЃП
ЃЈ5ЃЉаДГіnВуЕФСљБпаЮЕуеѓЕФзмЕуЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌOЮЊзјБъдЕуЃЌЕуA(1ЃЌ5)КЭЕуB(mЃЌ1)ОљдкЗДБШР§КЏЪ§yЃН ![]() ЭМЯѓЩЯЃЎ
ЭМЯѓЩЯЃЎ
ЃЈ1ЃЉЧѓmЃЌkЕФжЕЃЛ
ЃЈ2ЃЉЩшжБЯпABгыxжсНЛгкЕуCЃЌЧѓЁїAOCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(вЛ)ЮЪЬтЬсГіЃКШчКЮАбnИіБпГЄЮЊ1ЕФе§ЗНаЮЃЌМєЦДГЩвЛИіДѓе§ЗНаЮЃП
(Жў)НтОіЗНЗЈ
ЬНОПвЛЃКШєnЪЧЭъШЋЦНЗНЪ§ЃЌЮвУЧВЛгУМєЧааЁе§ЗНаЮЃЌПЩжБНгНЋаЁе§ЗНаЮЦДГЩвЛИіДѓе§ЗНаЮЃЌШчЭМ(1)ЃЌгУЫФИіБпГЄЮЊ1ЕФаЁе§ЗНаЮПЩвдЦДГЩвЛИіДѓе§ЗНаЮЃЎ
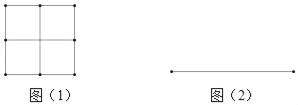
ЮЪЬт1ЃКЧыгУ9ИіБпГЄЮЊ1ЕФаЁе§ЗНаЮдкЭМ(2)ЕФЮЛжУЦДГЩвЛИіДѓе§ЗНаЮЃЎ
ЬНОПЖўЃКШєnЃН2ЃЌ5ЃЌ10ЃЌ13ЕШетаЉЪ§ЃЌЖМПЩвдгУСНИіе§ећЪ§ЕФЦНЗНКЭРДБэЪОЃЌвдnЃН5ЮЊР§ЃЌгУ5ИіБпГЄЮЊ1ЕФаЁе§ЗНаЮМєЦДГЩвЛИіДѓе§ЗНаЮЃЎ
(1)МЦЫуЃКЦДГЩЕФДѓе§ЗНаЮЕФУцЛ§ЮЊ5ЃЌБпГЄЮЊ![]() ЃЌПЩБэЪОГЩ
ЃЌПЩБэЪОГЩ![]() ЃЛ
ЃЛ
(2)МєЧаЃКШчЭМ(3)НЋ5ИіаЁе§ЗНаЮАДШчЭМЫљЪОЗжГЩ5ВПЗжЃЌащЯпЮЊМєЧаЯпЃЛ
(3)ЦДЭМЃКвдЭМ(3)жаЕФащЯпЮЊБпЃЌЦДГЩвЛИіБпГЄЮЊ![]() ЕФДѓе§ЗНаЮЃЌШчЭМ(4)ЃЎ
ЕФДѓе§ЗНаЮЃЌШчЭМ(4)ЃЎ
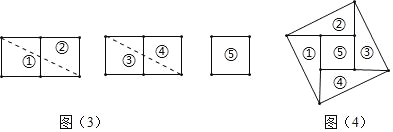
ЮЪЬт2ЃКЧыЗТееЩЯУцЕФбаОПЗНЪНЃЌгУ13ИіБпГЄЮЊ1ЕФаЁе§ЗНаЮМєЦДГЩвЛИіДѓе§ЗНаЮЃЛ
(1)МЦЫуЃКЦДГЩЕФДѓе§ЗНаЮЕФУцЛ§ЮЊ____ЃЌБпГЄЮЊ_____ЃЌПЩБэЪОГЩ____ЃЛ
(2)МєЧаЃКЧыЗТееЭМ(3)ЕФЗНЗЈЃЌдкЭМ(5)ЕФЮЛжУЛГіЭМаЮЃЎ
(3)ЦДЭМЃКЧыЗТееЭМ(4)ЕФЗНЗЈЃЌдкЭМ(6)ЕФЮЛжУГіЦДГЩЕФЭМЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com