
【题目】如图是二次函数 ![]() 图象的一部分,对称轴为
图象的一部分,对称轴为 ![]() ,且经过点(2,0)下列说法:①abc<0;②-2b+c=0;③4a+2b+c<0;④若(-
,且经过点(2,0)下列说法:①abc<0;②-2b+c=0;③4a+2b+c<0;④若(- ![]() ,y1),(
,y1),( ![]() ,y2)是抛物线上的两点,则y1<y2;⑤
,y2)是抛物线上的两点,则y1<y2;⑤ ![]() >m(am+b)其中(m≠
>m(am+b)其中(m≠ ![]() )其中说法正确的是( )
)其中说法正确的是( )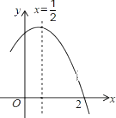
A.①②④⑤
B.③④
C.①③
D.①②⑤
【答案】A
【解析】根据抛物线开口方向及与y轴的交点的位置,可知a<0,c>0,根据对称轴的位置在y轴的右侧,由“左同右异”可知a、b异号,得出b>0,abc<0,故①正确;
根据抛物线的对称轴为直线x=-![]() =
=![]() 得出a=-b①,因为x=2时y=0.得4a+2b+c=0②,将①代入②得-2b+c=0,故②正确;
得出a=-b①,因为x=2时y=0.得4a+2b+c=0②,将①代入②得-2b+c=0,故②正确;
根据x-2时y=0得出4a+2b+c=0,故③错误;
∵点(-![]() ,y1)离对称轴要比(
,y1)离对称轴要比( ![]() ,y2)离对称轴远,∴y1<y2,故④正确;
,y2)离对称轴远,∴y1<y2,故④正确;
当x=![]() 时,y有最大值,所以
时,y有最大值,所以 ![]() a +
a + ![]() b+c>am2+bm+c(m≠
b+c>am2+bm+c(m≠ ![]() ),即
),即 ![]() a +
a + ![]() b>m(am+b)(m≠
b>m(am+b)(m≠ ![]() )。故⑤正确。
)。故⑤正确。
根据抛物线开口方向及与y轴的交点的位置,可知a<0,c>0,根据对称轴的位置在y轴的右侧,由“左同右异”可知a、b异号。得出b>0 ,即可对①作出判断;根据抛物线的对称轴得出a=-b,再结合x=2时y=0,即可对②作出判断;根据x-2时y=0得出4a+2b+c=0,即可对③作出判断;根据二次函数的性质可对④作出判断;根据二次函数的性质,当x=![]() ,y有最大值,可对⑤作出判断。从而得出正确选项。
,y有最大值,可对⑤作出判断。从而得出正确选项。


科目:初中数学 来源: 题型:
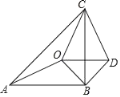
【题目】如图,△ABC是等腰直角三角形,AB=BC,O是△ABC内部的一个动点,△OBD是等腰直角三角形,OB=BD.
(1)求证:∠AOB=∠CDB;
(2)若△COD是等腰三角形,∠AOC=140°,求∠AOB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了个圆形喷水池,在水池中心竖直安装了一根高为2米的喷水管,它喷出的抛物线形水柱在与水池中心的水平距离为1米处达到最高,水柱落地处离池中心3米.
(1)请你建立适当的平面直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度的多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
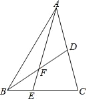
【题目】如图,△ABC中,点E是BC上的一点,EC=2BE,点D是AC的中点.若△ABC的面积S△ABC=12,则S△ADF﹣S△BEF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山地自行车越来越受中学生的喜爱.一网店经营的一个型号山地自行车,今年一月份销售额为30000元,二月份每辆车售价比一月份每辆车售价降价100元,若销售的数量与上一月销售的数量相同,则销售额是27000元.
(1)求二月份每辆车售价是多少元?
(2)为了促销,三月份每辆车售价比二月份每辆车售价降低了10%销售,网店仍可获利35%,求每辆山地自行车的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[知识生成]通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
例如:如图①是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
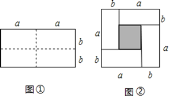
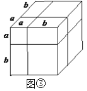
(1)图②中阴影部分的正方形的边长是________________;
(2)请用两种不同的方法求图②中阴影部分的面积:
方法1:________________________;方法2:_______________________;
(3)观察图②,请你写出(a+b)2、![]() 、
、![]() 之间的等量关系是____________________________________________;
之间的等量关系是____________________________________________;
(4)根据(3)中的等量关系解决如下问题:若![]() ,
,![]() ,则
,则![]() =
=
[知识迁移]
类似地,用两种不同的方法计算同一几何体的体积,也可以得到一个恒等式.
(5)根据图③,写出一个代数恒等式:____________________________;
(6)已知![]() ,
,![]() ,利用上面的规律求
,利用上面的规律求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC顶点的坐标分别是A(﹣1,3)、B(﹣5,1)、C(﹣2,﹣2).
(1)画出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′各顶点的坐标;
(2)求出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.
(1)求证:ED∥AC;
(2)连接AE,试证明:ABCD=AEAC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com