
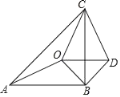
【题目】如图,△ABC是等腰直角三角形,AB=BC,O是△ABC内部的一个动点,△OBD是等腰直角三角形,OB=BD.
(1)求证:∠AOB=∠CDB;
(2)若△COD是等腰三角形,∠AOC=140°,求∠AOB的度数.
【答案】(1)详见解析;(2)∠AOB的度数为110°或95°或125°.
【解析】
(1)根据等腰直角三角形的性质和全等三角形的判定和性质解答即可;
(2)设∠AOB的度数为x,分三种情况进行解答即可.
(1)∵△ABC和△OBD是等腰直角三角形,
∴AB=BC,OB=BD,∠ABC=∠OBD=90°,
∵∠ABO+∠OBC=∠CBD+∠OBC,
∴∠ABO=∠CBD,
在△ABO和△CBD中
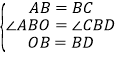 ,
,
∴△ABO≌△CBD(SAS),
∴∠AOB=∠CDB;
(2)设∠AOB的度数为x,则∠CDB=x,∠CDO=x﹣45°,
∠COD=∠COB﹣∠DOB=360°﹣140°﹣x﹣45°=175°﹣x,
∠OCD=180°﹣∠CDO﹣∠COD=50°,
①当∠CDO=∠COD时,x﹣45°=175°﹣x,解得:x=110°,
②当∠CDO=∠OCD时,x﹣45°=50°,解得:x=95°,
③当∠COD=∠OCD时,175°﹣x=50°,解得:x=125°,
故∠AOB的度数为110°或95°或125°.


科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线移动(即沿长方形移动一周).

(1)写出B点的坐标;
(2)当点P移动3秒时,求三角形OAP的面积;
(3)在移动过程中,当点P到x轴距离为4个单位长度时,求点P移动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
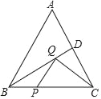
【题目】如图,等边△ABC的周长为18cm,BD为AC边上的中线,动点P,Q分别在线段BC,BD上运动,连接CQ,PQ,当BP长为_____cm时,线段CQ+PQ的和为最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
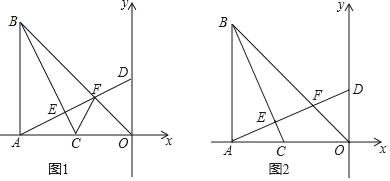
【题目】如图,在Rt△ABO中,∠BAO=90°,AO=AB,BO=8![]() ,点A的坐标(﹣8,0),点C在线段AO上以每秒2个单位长度的速度由A向O运动,运动时间为t秒,连接BC,过点A作AD⊥BC,垂足为点E,分别交BO于点F,交y轴于点 D.
,点A的坐标(﹣8,0),点C在线段AO上以每秒2个单位长度的速度由A向O运动,运动时间为t秒,连接BC,过点A作AD⊥BC,垂足为点E,分别交BO于点F,交y轴于点 D.
(1)用t表示点D的坐标 ;
(2)如图1,连接CF,当t=2时,求证:∠FCO=∠BCA;
(3)如图2,当BC平分∠ABO时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程满足方程组![]() .
.
(1)若x﹣y=2,求m的值;
(2)若x,y,m均为非负数,求m的取值范围,并化简式子|m﹣3|+|m﹣4|;
(3)在(2)的条件下求s=2x﹣3y+m的最小值及最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 交x轴于点A,交y轴于点B,交直线
交x轴于点A,交y轴于点B,交直线![]() 于点C,点D与点B关于x轴对称,连接AD交直线
于点C,点D与点B关于x轴对称,连接AD交直线![]() 于点E.
于点E.
![]() 填空:
填空:![]() ______.
______.
![]() 求直线AD的解析式;
求直线AD的解析式;
![]() 在x轴上存在一点P,则
在x轴上存在一点P,则![]() 的和最小为______;
的和最小为______;![]() 直接填空即可
直接填空即可![]()
![]() 当
当![]() 时,点Q为y轴上的一个动点,使得
时,点Q为y轴上的一个动点,使得![]() 为等腰直角三角形,求点Q的坐标.
为等腰直角三角形,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
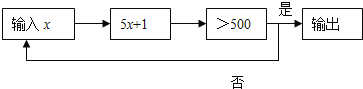
【题目】按下面程序计算,即根据输入的![]() 判断
判断![]() 是否大于500,若大于500则输出,结束计算,若不大于500,则以现在的
是否大于500,若大于500则输出,结束计算,若不大于500,则以现在的![]() 的值作为新的
的值作为新的![]() 的值,继续运算,循环往复,直至输出结果为止.若开始输入
的值,继续运算,循环往复,直至输出结果为止.若开始输入![]() 的值为正整数,最后输出的结果为656,则满足条件的所有
的值为正整数,最后输出的结果为656,则满足条件的所有![]() 的值是__.
的值是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数 ![]() 图象的一部分,对称轴为
图象的一部分,对称轴为 ![]() ,且经过点(2,0)下列说法:①abc<0;②-2b+c=0;③4a+2b+c<0;④若(-
,且经过点(2,0)下列说法:①abc<0;②-2b+c=0;③4a+2b+c<0;④若(- ![]() ,y1),(
,y1),( ![]() ,y2)是抛物线上的两点,则y1<y2;⑤
,y2)是抛物线上的两点,则y1<y2;⑤ ![]() >m(am+b)其中(m≠
>m(am+b)其中(m≠ ![]() )其中说法正确的是( )
)其中说法正确的是( )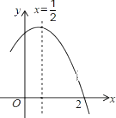
A.①②④⑤
B.③④
C.①③
D.①②⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为坐标原点,点A(1,5)和点B(m,1)均在反比例函数y= ![]() 图象上.
图象上.
(1)求m,k的值;
(2)设直线AB与x轴交于点C,求△AOC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com