
����Ŀ����ͼ����Rt��ABO�У���BAO��90����AO��AB��BO��8![]() ����A�����꣨��8��0������C���߶�AO����ÿ��2����λ���ȵ��ٶ���A��O�˶����˶�ʱ��Ϊt�룬����BC������A��AD��BC������Ϊ��E���ֱ�BO�ڵ�F����y���ڵ� D��
����A�����꣨��8��0������C���߶�AO����ÿ��2����λ���ȵ��ٶ���A��O�˶����˶�ʱ��Ϊt�룬����BC������A��AD��BC������Ϊ��E���ֱ�BO�ڵ�F����y���ڵ� D��
��1����t��ʾ��D�������� ����
��2����ͼ1������CF����t��2ʱ����֤����FCO����BCA��
��3����ͼ2����BCƽ�֡�ABOʱ����t��ֵ��
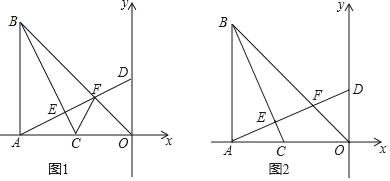
���𰸡���1����0��2t������2������������3��t=4��![]() ��1��
��1��
��������
��1������֪������֤����ABC�ա�OAD������ȫ�������ε����ʼ��������D�����ꣻ
��2���ɣ�1���Ľ��ۿ�֤����FOD�ա�FOC���Ӷ���FCO����FDO���ٸ��ݣ�1���С�ABC�ա�OAD���ɵá�ACB����ADO��������FCO����ACB��֤��
��3����AB��ȡһ��K��ʹ��AK��AC������CK����AK��AC��m����CK��![]() m�����ݽ�ƽ���ߵ����ʺ���������ǺͶ����ɵ�KB��KC��
m�����ݽ�ƽ���ߵ����ʺ���������ǺͶ����ɵ�KB��KC��![]() m���Ӷ����m��ֵ������t��ֵҲ�����.
m���Ӷ����m��ֵ������t��ֵҲ�����.
�⣺��1����AD��BC��
���AEB��90������BAC����AOD��
���ABC+��BAE��90������BAE+��OAD��90����
���ABC����OAD��
��AB��OA��
���ABC�ա�OAD��ASA����
��OD��AC��2t��
��D��0��2t����
�ʴ�Ϊ��0��2t����
��2����ͼ1�У�
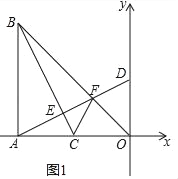
��AB��AO����BAO��90����OB��![]() ��
��
��AB��AO��8��
��t��2��
��AC��OD��4��
��OC��OD��4��
��OF��OF����FOD����FOC��
���FOD�ա�FOC��SAS����
���FCO����FDO��
�ߡ�ABC�ա�OAD��
���ACB����ADO��
���FCO����ACB��
��3����ͼ2�У���AB��ȡһ��K��ʹ��AK��AC������CK����AK��AC��m����CK��![]() m��
m��
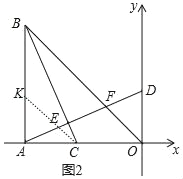
��CBƽ�֡�ABO��
���ABC��22.5����
�ߡ�AKC��45������ABC+��KCB��
���KBC����KCB��22.5����
��KB��KC��![]() m��
m��
��m+![]() m��8��
m��8��
��m��8��![]() ����
����
��t��![]() ��4��
��4��![]() ��1����
��1����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ABCD�У�E��CD����һ�㣬
��1������ADE�Ƶ�A��˳ʱ�뷽����ת��ʹAD��AB�غϣ��õ���ABF����ͼ1��ʾ���۲��֪����DE��ȵ��߶��� �� ��AFB=�� .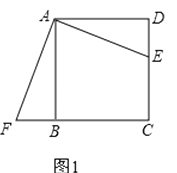
��2����ͼ2��������ABCD�У�P��Q�ֱ���BC��CD���ϵĵ㣬�ҡ�PAQ=45�㣬��ͨ����ת�ķ�ʽ˵����DQ+BP=PQ.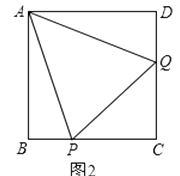
��3���ڣ�2�����У�����BD�ֱ�AP��AQ��M��N���㻹������ת��˼��˵��BM2+DN2=MN2 �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��DF�ֱ��ǡ�ABD�͡�ACD�ĸߡ���֤��AD��ֱƽ��EF��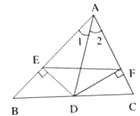
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�![]() �У�
��![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]()
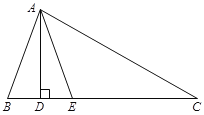
��1����![]() �Ķ�����
�Ķ�����
��2��̽����С����Ϊ���ֻ֪��![]() ��Ҳ�ܵó�
��Ҳ�ܵó�![]() �Ķ���������д�������̣�
�Ķ���������д�������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
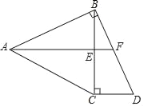
����Ŀ����ͼ���ڵ�����ABC�У�AB��AC������B��BD��AB������C��CD��BC�������ཻ�ڵ�D��AFƽ�֡�BAC��BC�ڵ�E����BD�ڵ�F��
��1������BAC��68�������DBC��
��2����֤����FΪBD�е㣻
��3����AC��BD����CD��3�����ı���ABDC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
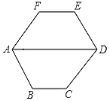
����Ŀ����ͼ��������ABCDEF���ڽǶ���ȣ���FAD��60����
��1�����ADE�Ķ�����
��2����֤��EF��BC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
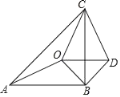
����Ŀ����ͼ����ABC�ǵ���ֱ�������Σ�AB��BC��O�ǡ�ABC�ڲ���һ�����㣬��OBD�ǵ���ֱ�������Σ�OB��BD��
��1����֤����AOB����CDB��
��2������COD�ǵ��������Σ���AOC��140�������AOB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ũ��Ľ���;ɳǵĸ��죬���ǵļ�Խ��Խ������С���Ҹ����㳡���������˸�Բ����ˮ�أ���ˮ��������ֱ��װ��һ����Ϊ2����ˮ�ܣ����������������ˮ������ˮ�����ĵ�ˮƽ����Ϊ1�״��ﵽ��ߣ�ˮ����ش��������3�ף�
��1�����㽨���ʵ���ƽ��ֱ������ϵ�������ˮ�������ߵĺ�������ʽ��
��2�����ˮ�������߶ȵĶ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC���������ֱ���A����1��3����B����5��1����C����2����2����
��1��������ABC����y��ԳƵ���A��B��C������д����A��B��C������������ꣻ
��2�������ABC�������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com