
【题目】如图,在△![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]()
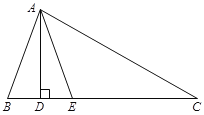
(1)求![]() 的度数;
的度数;
(2)探究:小明认为如果只知道![]() ,也能得出
,也能得出![]() 的度数.请你写出求解过程.
的度数.请你写出求解过程.
【答案】(1)20°;(2)20°,理由见解析
【解析】
(1)利用三角形的内角和定理求出∠BAC,再利用角平分线定义求∠BAE;求出∠BAD,就可知道∠DAE的度数;
(2)根据AE平分∠BAC,得到∠BAE.再根据垂直定义,在直角△ABD中,可以求得∠BAD,即可求得∠DAE=![]() (∠B-∠C).
(∠B-∠C).
(1)∵![]()
∴∠BDA=90°
∵![]()
∴∠BAD=20°
∵![]()
∴∠BAC=80°
∵![]() 平分
平分![]()
∴![]() =
=![]() =40°
=40°
∴∠DAE=∠BAE-∠BAD=20°
(2)∵![]()
∴∠BDA=90°
∴∠BAD=90°-∠B
∵![]() 平分
平分![]()
∴∠BAE=![]() =
=![]()
∴∠DAE=∠BAE-∠BAD=![]() -(90°-∠B)
-(90°-∠B)
=![]()
∵![]()
∴∠DAE=20°


科目:初中数学 来源: 题型:
【题目】细心观察图形,认真分析各式,然后解答问题.
OA22=![]() ,
,![]() ;
;
OA32=12+![]() ,
,![]() ;
;
OA42=12+![]() ,
,![]() …
…
(1)请用含有n(n是正整数)的等式表示上述变规律:OAn2等于多少;Sn等于多少.
(2)求出OA10的长.
(3)若一个三角形的面积是![]() ,计算说明他是第几个三角形?
,计算说明他是第几个三角形?
(4)求出S12+S22+S32+…+S102的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
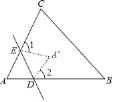
【题目】如图,在折纸活动中,小李制作了一张△ABC的纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A'重合.
(1)若∠B=50°,∠C=60°,求∠A的度数;
(2)若∠1+∠2=130°,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
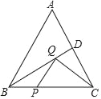
【题目】如图,等边△ABC的周长为18cm,BD为AC边上的中线,动点P,Q分别在线段BC,BD上运动,连接CQ,PQ,当BP长为_____cm时,线段CQ+PQ的和为最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图表示玲玲骑自行车离家的距离与时间的关系.她9点离开家,15点回到家,请根据图象回答下列问题:

(1)玲玲到达离家最远的地方是什么时间?她离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)第一次休息时,她离家多远?
(4)11点~12点她骑车前进了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
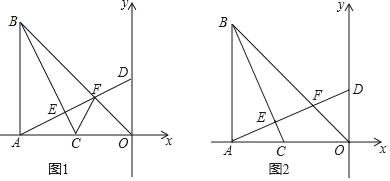
【题目】如图,在Rt△ABO中,∠BAO=90°,AO=AB,BO=8![]() ,点A的坐标(﹣8,0),点C在线段AO上以每秒2个单位长度的速度由A向O运动,运动时间为t秒,连接BC,过点A作AD⊥BC,垂足为点E,分别交BO于点F,交y轴于点 D.
,点A的坐标(﹣8,0),点C在线段AO上以每秒2个单位长度的速度由A向O运动,运动时间为t秒,连接BC,过点A作AD⊥BC,垂足为点E,分别交BO于点F,交y轴于点 D.
(1)用t表示点D的坐标 ;
(2)如图1,连接CF,当t=2时,求证:∠FCO=∠BCA;
(3)如图2,当BC平分∠ABO时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 交x轴于点A,交y轴于点B,交直线
交x轴于点A,交y轴于点B,交直线![]() 于点C,点D与点B关于x轴对称,连接AD交直线
于点C,点D与点B关于x轴对称,连接AD交直线![]() 于点E.
于点E.
![]() 填空:
填空:![]() ______.
______.
![]() 求直线AD的解析式;
求直线AD的解析式;
![]() 在x轴上存在一点P,则
在x轴上存在一点P,则![]() 的和最小为______;
的和最小为______;![]() 直接填空即可
直接填空即可![]()
![]() 当
当![]() 时,点Q为y轴上的一个动点,使得
时,点Q为y轴上的一个动点,使得![]() 为等腰直角三角形,求点Q的坐标.
为等腰直角三角形,求点Q的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com