
【题目】如图,在平面直角坐标系中,直线![]() 交x轴于点A,交y轴于点B,交直线
交x轴于点A,交y轴于点B,交直线![]() 于点C,点D与点B关于x轴对称,连接AD交直线
于点C,点D与点B关于x轴对称,连接AD交直线![]() 于点E.
于点E.
![]() 填空:
填空:![]() ______.
______.
![]() 求直线AD的解析式;
求直线AD的解析式;
![]() 在x轴上存在一点P,则
在x轴上存在一点P,则![]() 的和最小为______;
的和最小为______;![]() 直接填空即可
直接填空即可![]()
![]() 当
当![]() 时,点Q为y轴上的一个动点,使得
时,点Q为y轴上的一个动点,使得![]() 为等腰直角三角形,求点Q的坐标.
为等腰直角三角形,求点Q的坐标.

【答案】(1)12;(2)![]() ;(3)
;(3)![]() ;(4)点Q的坐标为
;(4)点Q的坐标为![]() 或
或![]() 或
或![]() .
.
【解析】
![]() 分别计算A、B、D三点的坐标,可得OA和BD的长,根据三角形面积公式可得结论;
分别计算A、B、D三点的坐标,可得OA和BD的长,根据三角形面积公式可得结论;
![]() 利用待定系数法可得直线AD的解析式;
利用待定系数法可得直线AD的解析式;
![]() 根据轴对称的最短路径先确认P的位置:连接BE交x轴于P,此时,
根据轴对称的最短路径先确认P的位置:连接BE交x轴于P,此时,![]() 最小,即是BE的长,利用勾股定理可计算BE的长,最后将其配方后,根据二次函数的最值可得结论;
最小,即是BE的长,利用勾股定理可计算BE的长,最后将其配方后,根据二次函数的最值可得结论;
![]() 存在三种情况:分别以Q、E、C三个顶点为直角顶点,画图可得Q的坐标.
存在三种情况:分别以Q、E、C三个顶点为直角顶点,画图可得Q的坐标.
![]() 如图1,
如图1,![]() 直线
直线![]() 交x轴于点A,交y轴于点B,
交x轴于点A,交y轴于点B,
令![]() ,
,![]() ,
,
![]() ,
,
令![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 点D与点B关于x轴对称,
点D与点B关于x轴对称,
![]() ,
,
![]() ,
,
故答案为:12;
![]() 如图1,设直线AD的解析式为
如图1,设直线AD的解析式为![]() ,由
,由![]() 知,
知,![]() ,
,![]() ,
,
![]() ,
,
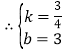 ,
,
![]() 直线AD的解析式为
直线AD的解析式为![]() ;
;
![]() 如图2,由
如图2,由![]() 知,直线AD的解析式为
知,直线AD的解析式为![]() ,
,
![]() 直线CE:
直线CE:![]() ,
,
![]() ,
,
![]() 点D与点B关于x轴对称,
点D与点B关于x轴对称,
![]() 连接BE交x轴于P,
连接BE交x轴于P,
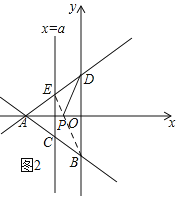
此时,![]() 最小,最小值为BE,
最小,最小值为BE,
![]() ,
,
![]() 的最小值是
的最小值是![]() ,
,
则![]() 的和最小为
的和最小为![]() ;
;
故答案为:![]() ;
;
![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
设![]() ,
,![]() ,
,
![]() 为等腰直角三角形时,存在以下三种情况:
为等腰直角三角形时,存在以下三种情况:
![]() 当E为直角顶点时,如图3,
当E为直角顶点时,如图3,
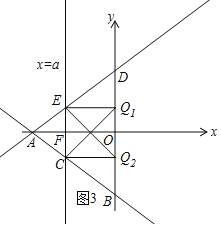
![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,
![]() ;
;
![]() 当C为直角顶点时,如图3,同理得
当C为直角顶点时,如图3,同理得![]() ;
;
![]() 当Q为直角顶点时,如图4,
当Q为直角顶点时,如图4,
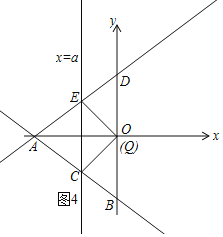
此时Q与O重合,![]()
综上,点Q的坐标为![]() 或
或![]() 或
或![]() .
.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2![]() EF,则正方形ABCD的面积为( )
EF,则正方形ABCD的面积为( )

A. 14SB. 13SC. 12SD. 11S
查看答案和解析>>
科目:初中数学 来源: 题型:
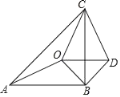
【题目】如图,△ABC是等腰直角三角形,AB=BC,O是△ABC内部的一个动点,△OBD是等腰直角三角形,OB=BD.
(1)求证:∠AOB=∠CDB;
(2)若△COD是等腰三角形,∠AOC=140°,求∠AOB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线 ![]() 与x轴的交点为A,B(点A在点B的左侧),与y轴的交点为C,连结BC.点M是抛物线上A,C之间的一个动点,过点M作MN∥BC,分别交x轴、抛物线于D,N,过点M作EF⊥x轴,垂足为F,并交直线BC于点E,
与x轴的交点为A,B(点A在点B的左侧),与y轴的交点为C,连结BC.点M是抛物线上A,C之间的一个动点,过点M作MN∥BC,分别交x轴、抛物线于D,N,过点M作EF⊥x轴,垂足为F,并交直线BC于点E,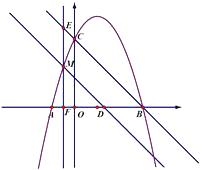
(1)求点A,B,C的坐标.
(2)当点M恰好是EF的中点,求BD的长.
(3)连接DE,记△DEM,△BDE的面积分别为S1,S2 ,当BD=1时,请求S2-S1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了个圆形喷水池,在水池中心竖直安装了一根高为2米的喷水管,它喷出的抛物线形水柱在与水池中心的水平距离为1米处达到最高,水柱落地处离池中心3米.
(1)请你建立适当的平面直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度的多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山地自行车越来越受中学生的喜爱.一网店经营的一个型号山地自行车,今年一月份销售额为30000元,二月份每辆车售价比一月份每辆车售价降价100元,若销售的数量与上一月销售的数量相同,则销售额是27000元.
(1)求二月份每辆车售价是多少元?
(2)为了促销,三月份每辆车售价比二月份每辆车售价降低了10%销售,网店仍可获利35%,求每辆山地自行车的进价是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com