
【题目】如图,在平面直角坐标系中,抛物线 ![]() 与x轴的交点为A,B(点A在点B的左侧),与y轴的交点为C,连结BC.点M是抛物线上A,C之间的一个动点,过点M作MN∥BC,分别交x轴、抛物线于D,N,过点M作EF⊥x轴,垂足为F,并交直线BC于点E,
与x轴的交点为A,B(点A在点B的左侧),与y轴的交点为C,连结BC.点M是抛物线上A,C之间的一个动点,过点M作MN∥BC,分别交x轴、抛物线于D,N,过点M作EF⊥x轴,垂足为F,并交直线BC于点E,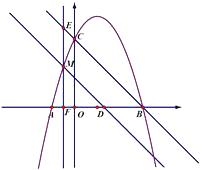
(1)求点A,B,C的坐标.
(2)当点M恰好是EF的中点,求BD的长.
(3)连接DE,记△DEM,△BDE的面积分别为S1,S2 ,当BD=1时,请求S2-S1的值.
【答案】
(1)解:∵抛物线 y=x2+2x+3 与x轴的交点为A,B(点A在点B的左侧),
∴令y=0,即x2+2x+3 =0,
∴x1=-1,x2=3,
∴A(-1,0) ,B(3,0),
又∵抛物线与y轴的交点为C,
∴C(0,3),
(2)解:设BC的函数解析式为y=kx+b,
∵ B(3,0), C(0,3),
∴![]() ,
,![]() ,
,
∴BC的函数解析式为:y=-x+3,
∵点M是抛物线上A,C之间的一个动点,
∴设 M(m,m2+2m+3) (-1![]() m
m![]() 0),则 E(m,m+3),F(m,0),
0),则 E(m,m+3),F(m,0),
∴EF=-m+3,MF=m2+2m+3,
又∵M为EF中点,
∴ 2(m2+2m+3)=m+3 ,
∴ m1=3,m2=![]() ,
,
又∵-1![]() m
m![]() 0,
0,
∴m=![]() ,
,
∴F(-![]() ,0),
,0),
∴BF=3-(-![]() )=
)=![]() ,
,
又∵MD∥BC,
∴D为BF的中点,
∴ BD=![]() BF=
BF=![]() ×
×![]() =
=![]() .
.
(3)解:由图形可知,D在B点左侧,当BD=1时,D点坐标为(2,0),
由(2)知BC的函数解析式为:y=-x+3,
又∵MD∥BC,
∴MD的函数解析式为: y=x+2 .
∴![]() ,
,
解得: x1=![]() ,x2=
,x2=![]() (舍去),
(舍去),
∴M (![]() ,
,![]() ) ,E (
) ,E (![]() ,
,![]() ) ,
) ,
∴ME=1,DF=![]() ,EF=
,EF=![]() .
.
∴ S2S1=![]() ×1×
×1×![]()
![]() ×1×
×1×![]() =
=![]() .
.
【解析】(1)根据抛物线 y=x2+2x+3 与x轴的交点为A,B(点A在点B的左侧),与y轴的交点为C,分别令x=0,y=0即可求出A ,B,C坐标.
(2)由B、C的坐标用待定系数法即可求得直线BC的解析式,由点M是抛物线上A,C之间的一个动点,可设 M(m,m2+2m+3) (-1![]() m
m![]() 0),则 E(m,m+3),F(m,0),从而得到EF,MF的长,再由M为EF中点可得关于m的关系式,从而求出m,得出BF的长,再由MD∥BC,根据三角形中位线定理得出D为BF的中点,即BD=
0),则 E(m,m+3),F(m,0),从而得到EF,MF的长,再由M为EF中点可得关于m的关系式,从而求出m,得出BF的长,再由MD∥BC,根据三角形中位线定理得出D为BF的中点,即BD=![]() BF即可求得其值.
BF即可求得其值.
(3)由图形可知,D在B点左侧,当BD=1时,D点坐标为(2,0),由(2)知BC的函数解析式为:y=-x+3,根据MD∥BC得出MD的函数解析式为: y=x+2 ;再将MD解析式和抛物线联立求出M点坐标,从而得出E点坐标,由坐标得出ME,DF ,EF的长;再根据三角形面积公式得出S2S1值.
【考点精析】本题主要考查了确定一次函数的表达式和三角形的面积的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;三角形的面积=1/2×底×高才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①3x﹣1=0,②![]() x+1=0,③x﹣(3x+1)=﹣5中,不等式组
x+1=0,③x﹣(3x+1)=﹣5中,不等式组![]() 的关联方程是 ;(填序号)
的关联方程是 ;(填序号)
(2)若不等式组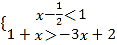 的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)
的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)
(3)若方程3﹣x=2x,3+x=2(x+![]() )都是关于x的不等式组
)都是关于x的不等式组![]() 的关联方程,直接写出m的取值范围.
的关联方程,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图表示玲玲骑自行车离家的距离与时间的关系.她9点离开家,15点回到家,请根据图象回答下列问题:

(1)玲玲到达离家最远的地方是什么时间?她离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)第一次休息时,她离家多远?
(4)11点~12点她骑车前进了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据表中的信息判断,下列语句中正确的是( )
x | 15 | 15.1 | 15.2 | 15.3 | 15.4 | 15.5 | 15.6 | 15.7 | 15.8 | 15.9 | 16 |
x2 | 225 | 228.01 | 231.04 | 234.09 | 237.16 | 240.25 | 243.36 | 246.49 | 249.64 | 252.81 | 256 |
A.![]()
B.235的算术平方根比15.3小
C.只有3个正整数n满足15.5![]()
D.根据表中数据的变化趋势,可以推断出16.12将比256增大3.19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 交x轴于点A,交y轴于点B,交直线
交x轴于点A,交y轴于点B,交直线![]() 于点C,点D与点B关于x轴对称,连接AD交直线
于点C,点D与点B关于x轴对称,连接AD交直线![]() 于点E.
于点E.
![]() 填空:
填空:![]() ______.
______.
![]() 求直线AD的解析式;
求直线AD的解析式;
![]() 在x轴上存在一点P,则
在x轴上存在一点P,则![]() 的和最小为______;
的和最小为______;![]() 直接填空即可
直接填空即可![]()
![]() 当
当![]() 时,点Q为y轴上的一个动点,使得
时,点Q为y轴上的一个动点,使得![]() 为等腰直角三角形,求点Q的坐标.
为等腰直角三角形,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:给定两个不等式组![]() 和
和![]() ,若不等式组
,若不等式组![]() 的任意一个解,都是不等式组
的任意一个解,都是不等式组![]() 的一个解,则称不等式组
的一个解,则称不等式组![]() 为不等式组
为不等式组![]() 的“子集”例如:不等式组:
的“子集”例如:不等式组:![]() 是:
是:![]() 的“子集”.
的“子集”.
(1)若不等式组:![]() ,
,![]() ,其中不等式组_________是不等式组
,其中不等式组_________是不等式组![]() 的“子集”(填
的“子集”(填![]() 或
或![]() );
);
(2)若关于![]() 的不等式组
的不等式组![]() 是不等式组
是不等式组![]() 的“子集”,则
的“子集”,则![]() 的取值范围是________;
的取值范围是________;
(3)已知![]() 为互不相等的整数,其中
为互不相等的整数,其中![]() ,
,![]() ,下列三个不等式组:
,下列三个不等式组:![]() ,
,![]() ,
,![]() 满足:
满足:![]() 是
是![]() 的“子集”且
的“子集”且![]() 是
是![]() 的“子集”,则
的“子集”,则![]() 的值为__________;
的值为__________;
(4)已知不等式组![]() 有解,且
有解,且![]() 是不等式组
是不等式组![]() 的“子集”,请写出
的“子集”,请写出![]() ,
,![]() 满足的条件:________________.
满足的条件:________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家发改委、工业和信息化部、财政部公布了“节能产品惠民工程”,公交公司积极响应将旧车换成节能环保公交车,计划购买A型和B型两种环保型公交车10辆,其中每台的价格、年载客量如表:
A型 | B型 | |
价格(万元/台) | x | y |
年载客量/万人次 | 60 | 100 |
若购买A型环保公交车1辆,B型环保公交车2辆,共需400万元;若购买A型环保公交车2辆,B型环保公交车1辆,共需350万元.
(1)求x、y的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保10辆公交车在该线路的年载客量总和不少于680万人次,问有哪几种购买方案?
(3)在(2)的条件下,哪种方案使得购车总费用最少?最少费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某场足球比赛中,球员甲从球门底部中心点O的正前方10m处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为3m时达到最高点,此时足球飞行的水平距离为6m.已知球门的横梁高为2.44m.
(1)在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
(2)守门员乙站在距离球门2m处,他跳起时手的最大摸高为2.52m,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com