
【题目】如图,O为坐标原点,点A(1,5)和点B(m,1)均在反比例函数y= ![]() 图象上.
图象上.
(1)求m,k的值;
(2)设直线AB与x轴交于点C,求△AOC的面积.
【答案】
(1)解:将A(1,5)和点B(m,1)代入y=![]() 得:
得:
m=5,k=5.
(2)解:设直AB所对应的一次函数关系式为:y=ax+b(a≠0),
将A(1,5)和点B(5,1)代入可得 ![]() ,
,
解得a=-1,b=6,
∴y=-x+6,
令y=0,得x=6,即OC=6,
S△AOC= ![]() OC×AE=
OC×AE= ![]() ×6×5=15.
×6×5=15.
【解析】(1)先将A(1,5)和点B(m,1)代入反比例函数解析式即可求出m、k的值。
(2)先根据A、B两点坐标求出直线AB的函数解析式,再根据y=0求出直线AB与x轴的交点C的坐标,根据三角形的面积公式即可求解。
【考点精析】本题主要考查了确定一次函数的表达式的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能正确解答此题.


科目:初中数学 来源: 题型:
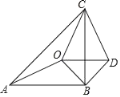
【题目】如图,△ABC是等腰直角三角形,AB=BC,O是△ABC内部的一个动点,△OBD是等腰直角三角形,OB=BD.
(1)求证:∠AOB=∠CDB;
(2)若△COD是等腰三角形,∠AOC=140°,求∠AOB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[知识生成]通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
例如:如图①是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
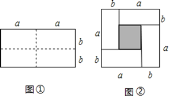
(1)图②中阴影部分的正方形的边长是________________;
(2)请用两种不同的方法求图②中阴影部分的面积:
方法1:________________________;方法2:_______________________;
(3)观察图②,请你写出(a+b)2、![]() 、
、![]() 之间的等量关系是____________________________________________;
之间的等量关系是____________________________________________;
(4)根据(3)中的等量关系解决如下问题:若![]() ,
,![]() ,则
,则![]() =
=
[知识迁移]
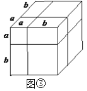
类似地,用两种不同的方法计算同一几何体的体积,也可以得到一个恒等式.
(5)根据图③,写出一个代数恒等式:____________________________;
(6)已知![]() ,
,![]() ,利用上面的规律求
,利用上面的规律求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC顶点的坐标分别是A(﹣1,3)、B(﹣5,1)、C(﹣2,﹣2).
(1)画出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′各顶点的坐标;
(2)求出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料会畅销、先用1800元购进一批这种饮料,面市后果然供不应求,又用8100元购进这种饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若两次进饮料都按同一价格销售,两批全部售完后,获利不少于2700元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并解决有关问题:
我们知道,|m|= .现在我们可以用这一结论来化简含有绝对值的代
.现在我们可以用这一结论来化简含有绝对值的代
数式,如化简代数式|m+1|+|m﹣2|时,可令 m+1=0 和 m﹣2=0,分别求得 m=﹣1,m=2(称﹣1,2 分别为|m+1|与|m﹣2|的零点值).在实数范围内, 零点值 m=﹣1 和 m=2 可将全体实数分成不重复且不遗漏的如下 3 种情况:
(1)m<﹣1;(2)﹣1≤m<2;(3)m≥2.从而化简代数式|m+1|+|m﹣2| 可分以下 3 种情况:
(1)当 m<﹣1 时,原式=﹣(m+1)﹣(m﹣2)=﹣2m+1;
(2)当﹣1≤m<2 时,原式=m+1﹣(m﹣2)=3;
(3)当 m≥2 时,原式=m+1+m﹣2=2m﹣1.
综上讨论,原式=
通过以上阅读,请你解决以下问题:
(1)分别求出|x﹣5|和|x﹣4|的零点值;
(2)化简代数式|x﹣5|+|x﹣4|;
(3)求代数式|x﹣5|+|x﹣4|的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.
(1)求证:ED∥AC;
(2)连接AE,试证明:ABCD=AEAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=90°,∠BCD=135°,且AB=3cm,BC=7cm,CD=5![]() cm,点M从点A出发沿折线A﹣B﹣C﹣D运动到点D,且在AB上运动的速度为
cm,点M从点A出发沿折线A﹣B﹣C﹣D运动到点D,且在AB上运动的速度为![]() cm/s,在BC上运动的速度为1cm/s,在CD上运动的速度为
cm/s,在BC上运动的速度为1cm/s,在CD上运动的速度为![]() cm/s,连接AM、DM,当点M运动时间为_____(s)时,△ADM是直角三角形.
cm/s,连接AM、DM,当点M运动时间为_____(s)时,△ADM是直角三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com