
【题目】(一)问题提出:如何把n个边长为1的正方形,剪拼成一个大正方形?
(二)解决方法
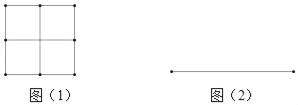
探究一:若n是完全平方数,我们不用剪切小正方形,可直接将小正方形拼成一个大正方形,如图(1),用四个边长为1的小正方形可以拼成一个大正方形.
问题1:请用9个边长为1的小正方形在图(2)的位置拼成一个大正方形.
探究二:若n=2,5,10,13等这些数,都可以用两个正整数的平方和来表示,以n=5为例,用5个边长为1的小正方形剪拼成一个大正方形.
(1)计算:拼成的大正方形的面积为5,边长为![]() ,可表示成
,可表示成![]() ;
;
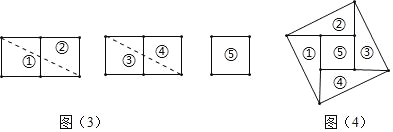
(2)剪切:如图(3)将5个小正方形按如图所示分成5部分,虚线为剪切线;
(3)拼图:以图(3)中的虚线为边,拼成一个边长为![]() 的大正方形,如图(4).
的大正方形,如图(4).
问题2:请仿照上面的研究方式,用13个边长为1的小正方形剪拼成一个大正方形;
(1)计算:拼成的大正方形的面积为____,边长为_____,可表示成____;
(2)剪切:请仿照图(3)的方法,在图(5)的位置画出图形.
(3)拼图:请仿照图(4)的方法,在图(6)的位置出拼成的图.
![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】[知识生成]通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
例如:如图①是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
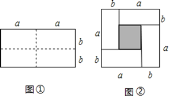
(1)图②中阴影部分的正方形的边长是________________;
(2)请用两种不同的方法求图②中阴影部分的面积:
方法1:________________________;方法2:_______________________;
(3)观察图②,请你写出(a+b)2、![]() 、
、![]() 之间的等量关系是____________________________________________;
之间的等量关系是____________________________________________;
(4)根据(3)中的等量关系解决如下问题:若![]() ,
,![]() ,则
,则![]() =
=
[知识迁移]
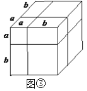
类似地,用两种不同的方法计算同一几何体的体积,也可以得到一个恒等式.
(5)根据图③,写出一个代数恒等式:____________________________;
(6)已知![]() ,
,![]() ,利用上面的规律求
,利用上面的规律求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并解决有关问题:
我们知道,|m|= .现在我们可以用这一结论来化简含有绝对值的代
.现在我们可以用这一结论来化简含有绝对值的代
数式,如化简代数式|m+1|+|m﹣2|时,可令 m+1=0 和 m﹣2=0,分别求得 m=﹣1,m=2(称﹣1,2 分别为|m+1|与|m﹣2|的零点值).在实数范围内, 零点值 m=﹣1 和 m=2 可将全体实数分成不重复且不遗漏的如下 3 种情况:
(1)m<﹣1;(2)﹣1≤m<2;(3)m≥2.从而化简代数式|m+1|+|m﹣2| 可分以下 3 种情况:
(1)当 m<﹣1 时,原式=﹣(m+1)﹣(m﹣2)=﹣2m+1;
(2)当﹣1≤m<2 时,原式=m+1﹣(m﹣2)=3;
(3)当 m≥2 时,原式=m+1+m﹣2=2m﹣1.
综上讨论,原式=
通过以上阅读,请你解决以下问题:
(1)分别求出|x﹣5|和|x﹣4|的零点值;
(2)化简代数式|x﹣5|+|x﹣4|;
(3)求代数式|x﹣5|+|x﹣4|的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.
(1)求证:ED∥AC;
(2)连接AE,试证明:ABCD=AEAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() +bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).
+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).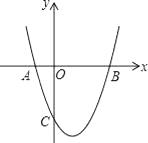
(1)求抛物线的解析式;
(2)D是y轴正半轴上的点,OD=3,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,
①试说明EF是圆的直径;
②判断△AEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个半径为r(r<1)的圆形纸片在边长为10的正六边形内任意运动,则在该六边形内,这个圆形纸片不能接触到的部分的面积是( )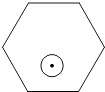
A.πr2
B.![]()
C.![]() r2
r2
D.![]() r2
r2
查看答案和解析>>
科目:初中数学 来源: 题型:
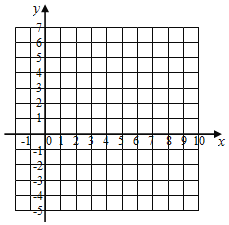
【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(6,c)三点,其中a,b,c满足关系式|a-2|+(b-3)2+![]() =0,
=0,
(1)求A.B.C的坐标;
(2)求三角形ABC的面积;
(3)在y轴上是否存在点P,使三角形APC的面积与三角形ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=90°,∠BCD=135°,且AB=3cm,BC=7cm,CD=5![]() cm,点M从点A出发沿折线A﹣B﹣C﹣D运动到点D,且在AB上运动的速度为
cm,点M从点A出发沿折线A﹣B﹣C﹣D运动到点D,且在AB上运动的速度为![]() cm/s,在BC上运动的速度为1cm/s,在CD上运动的速度为
cm/s,在BC上运动的速度为1cm/s,在CD上运动的速度为![]() cm/s,连接AM、DM,当点M运动时间为_____(s)时,△ADM是直角三角形.
cm/s,连接AM、DM,当点M运动时间为_____(s)时,△ADM是直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OMN与正方形ABCD,半径OM与边AB重合,弧MN的长等于AB的长,已知AB=2,扇形OMN沿着正方形ABCD逆时针滚动到点O首次与正方形的某顶点重合时停止,则点O经过的路径长 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com