
【题目】如图,在Rt△AOB中,∠AOB=90°,∠BAO=30°,以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点D.
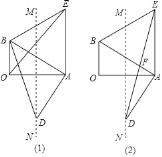
(1)连接BD,OE.求证:BD=OE;
(2)连接DE交AB于F.求证:F为DE的中点.
【答案】(1)见解析;(2)见解析.
【解析】
(1)连接OD,易证△ADO为等边三角形,再证△ABD≌△AEO即可.
(2)作EH⊥AB于H,先证△ABO≌△AEH,得AO=EH,再证△AFD≌△HFE即可.
证明:(1)连接OD,如图1,
∵△ABE是等边三角形,
∴AB=BE,∠EAB=60°,
∵DA⊥BA,
∴∠DAB=90°,
∵∠BAO=30°,
∴∠DAO=90°﹣30°=60°,
∴∠OAE=∠DAB,
∵MN垂直平分OA,
∴OD=DA,
∴△AOD是等边三角形,
∴DA=OA,
∴△ABD≌△AEO(SAS),
∴BD=OE;
(2)证明:如图2,作EH⊥AB于H,
∴∠EHA=∠DAF=90°,
∵AE=BE,
∴2AH=AB,
∵∠AOB=90°,∠BAO=30°,
∴2OB=AB,
∴AH=BO,
∴Rt△AEH≌Rt△BAO(HL),
∴EH=AO=AD,
∵∠EHF=∠DAF=90°,∠EFH=∠DFA,
∴△HFE≌△AFD(AAS),
∴EF=DF,
∴F为DE的中点.


科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系并说明理由;
(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.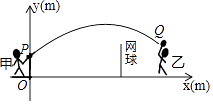
(1)当a=﹣ ![]() 时,①求h的值;
时,①求h的值;
②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 ![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
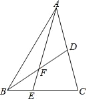
【题目】如图,△ABC中,点E是BC上的一点,EC=2BE,点D是AC的中点.若△ABC的面积S△ABC=12,则S△ADF﹣S△BEF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
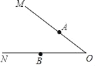
【题目】如图,已知∠MON,点A,B分别在OM,ON边上,且OA=OB.
(1)求作:过点A,B分别作OM,ON的垂线,两条垂线的交点记作点D(保留作图痕迹,不写作法);
(2)连接OD,若∠MON=50°,则∠ODB= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[知识生成]通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
例如:如图①是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
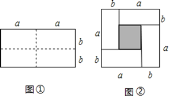
(1)图②中阴影部分的正方形的边长是________________;
(2)请用两种不同的方法求图②中阴影部分的面积:
方法1:________________________;方法2:_______________________;
(3)观察图②,请你写出(a+b)2、![]() 、
、![]() 之间的等量关系是____________________________________________;
之间的等量关系是____________________________________________;
(4)根据(3)中的等量关系解决如下问题:若![]() ,
,![]() ,则
,则![]() =
=
[知识迁移]
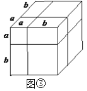
类似地,用两种不同的方法计算同一几何体的体积,也可以得到一个恒等式.
(5)根据图③,写出一个代数恒等式:____________________________;
(6)已知![]() ,
,![]() ,利用上面的规律求
,利用上面的规律求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点A、B表示的点分别为-6和3
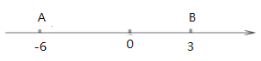
(1)若数轴上有一点P,它到A和点B的距离相等,则点P对应的数字是________(直接写出答案)
(2)在上问的情况下,动点Q从点P出发,以3个单位长度/秒的速度在数轴上向左移动,是否存在某一个时刻,Q点与B点的距离等于 Q点与A点的距离的2倍?若存在,求出点Q运动的时间,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料会畅销、先用1800元购进一批这种饮料,面市后果然供不应求,又用8100元购进这种饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若两次进饮料都按同一价格销售,两批全部售完后,获利不少于2700元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() +bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).
+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).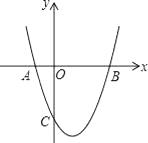
(1)求抛物线的解析式;
(2)D是y轴正半轴上的点,OD=3,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,
①试说明EF是圆的直径;
②判断△AEF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com