
【题目】找规律并解答问题.
(1)按下图方式摆放黑色围棋子,填一填,每个图共需几枚棋子.

图的顺序 |
|
|
|
|
|
需要的棋子数/枚 |
|
(2)根据你发现的规律,算一算第![]() 个图,共需要( )枚棋子.
个图,共需要( )枚棋子.
 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图所示放置,使得一直角边重合,连接BD,CE.
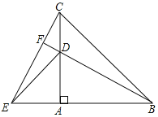
(1)求证:BD=CE;(2)延长BD,交CE于点F,求∠BFC的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们把对角线相等的四边形叫做和美四边形.
![]() 请举出一种你所学过的特殊四边形中是和美四边形的例子.
请举出一种你所学过的特殊四边形中是和美四边形的例子.
![]() 如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;
如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;
![]() 如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,
如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,![]() ,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天然气被公认是地球上最干净的化石能源,逐渐被广泛用于生产、生活中,2019年1月1日起,某天然气有限公司对居民生活用天然气进行调整,下表为2018年、2019年两年的阶梯价格
阶梯 | 用户年用气量 (单位:立方米) | 2018年单价 (单位:元/立方米) | 2019年单价 (单位:元/立方米) |
第一阶梯 | 0-300(含) |
| 3 |
第二阶梯 | 300-600(含) |
| 3.5 |
第三阶梯 | 600以上 |
| 5 |
(1)甲用户家2018年用气总量为280立方米,则总费用为 元(用含![]() 的代数式表示);
的代数式表示);
(2)乙用户家2018年用气总量为450立方米,总费用为1200元,求![]() 的值;
的值;
(3)在(2)的条件下,丙用户家2018年和2019年共用天然气1200立方米,2018年用气量大于2019年用气量,总费用为3625元,求该用户2018年和2019年分别用气多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中, △ABC的三个顶点的位置如图所示,点A'的坐标是
(-2,2), 现将△ABC平移,使点A变换为点A',点B′、C′分别是B、C的对应点。

(1)请画出平移后的像△A'B'C'(不写画法) ,并直接写出点B′、C′的坐标:
B′ ( ) 、C′ ( ) ;
(2)若△ABC 内部一点P的坐标为(a,b),则点P 的对应点P ′的坐标是 ( ) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解决问题
材料一:如果一个正整数的个位数字等于除个位数字之外的其他各位数字之和,则称这个数为“刀塔数”,比如:因1+2=3,所以123是“刀塔数”,同理,55,1315也是“刀塔数”.
材料二:形如![]() 的三位数叫“王者数”,其中x﹣2,x,x+2分别是这个数的百位数字,十位数字,个位数字.例如:135,468均为“王者数”
的三位数叫“王者数”,其中x﹣2,x,x+2分别是这个数的百位数字,十位数字,个位数字.例如:135,468均为“王者数”
问题:
(1)已知a既是“刀塔数”又是“王者数”,若数b(b>0)使10a+b为一个“刀塔数”,求b的最小值;
(2)已知一个五位“刀塔数”![]() 与一个“王者数”的和能被3整除,且c﹣a+d﹣b=4,证明
与一个“王者数”的和能被3整除,且c﹣a+d﹣b=4,证明![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2018春季环境整治活动中,某社区计划对面积为1600m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用5天.
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y关于x的函数关系式;
(3)若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,且甲乙两队施工的总天数不超过25天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【新知理解】
如图①,点C在线段AB上,图中共有三条线段AB、AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”.
线段的中点__________这条线段的“巧点”;(填“是”或“不是”).
若AB = 12cm,点C是线段AB的巧点,则AC=___________cm;
【解决问题】
(3) 如图②,已知AB=12cm.动点P从点A出发,以2cm/s的速度沿AB向点B匀速移动:点Q从点B出发,以1cm/s的速度沿BA向点A匀速移动,点P、Q同时出发,当其中一点到达终点时,运动停止,设移动的时间为t(s).当t为何值时,A、P、Q三点中其中一点恰好是另外两点为端点的线段的巧点?说明理由

![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com