
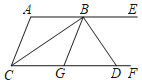
【题目】如图,AE∥CF,∠ACF的平分线交AE于点B,G是CF上的一点,∠GBE的平分线交CF于点D,且BD⊥BC,下列结论:①BC平分∠ABG;②AC∥BG;③与∠DBE互余的角有2个;④若∠A=α,则∠BDF=![]() .其中正确的有_____.(把你认为正确结论的序号都填上)
.其中正确的有_____.(把你认为正确结论的序号都填上)
【答案】①②④.
【解析】
求出∠EBD+∠ABC=90°,∠DBG+∠CBG=90°,求出∠ABC=∠GBC,根据角平分线的定义即可判断①;根据平行线的性质得出∠ABC=∠BCG,求出∠ACB=∠GBC,根据平行线的判定即可判断②;根据余角的定义即可判断③;根据平行线的性质得出∠EBG=∠A=α,求出∠EBD=![]() ∠EBG=
∠EBG=![]() α,根据平行线的性质得出∠EBD+∠BDF=180°,即可判断④.
α,根据平行线的性质得出∠EBD+∠BDF=180°,即可判断④.
∵BD⊥BC,
∴∠DBC=90°,
∴∠EBD+∠ABC=180°﹣90°=90°,∠DBG+∠CBG=90°,
∵BD平分∠EBG,
∴∠EBD=∠DBG,
∴∠ABC=∠GBC,
即BC平分∠ABG,故①正确;
∵AE∥CF,
∴∠ABC=∠BCG,
∵CB平分∠ACF,
∴∠ACB=∠BCG,
∵∠ABC=∠GBC,
∴∠ACB=∠GBC,
∴AC∥BG,故②正确;
与∠DBE互余的角有∠ABC,∠CBG,∠ACB,∠BCG,共4个,故③错误;
∵AC∥BG,∠A=α,
∴∠EBG=∠A=α,
∵∠EBD=∠DBG,
∴∠EBD=![]() ∠EBG=
∠EBG=![]() ,
,
∵AB∥CF,
∴∠EBD+∠BDF=180°,
∴∠BDF=180°﹣∠EBD=180°﹣![]() ,故④正确;
,故④正确;
故答案为:①②④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径是2,点A、B、C在⊙O上,若四边形OABC为菱形,则图中阴影部分面积为( )
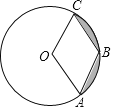
A. ![]() π﹣2
π﹣2![]() B.
B. ![]() π﹣
π﹣![]() C.
C. ![]() π﹣2
π﹣2![]() D.
D. ![]() π﹣
π﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为_____厘米/秒,△BPD与△CQP全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知P(1,2).
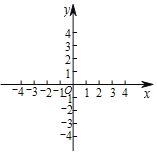
(1)在平面直角坐标系中描出点P(保留画图痕迹);
(2)如果将点P向左平移3个单位长度,再向上平移1个单位长度得到点P',则点P'的坐标为 .
(3)点A在坐标轴上,若S△OAP=2,直接写出满足条件的点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在三角形ABC中,D是BC上一点,且∠CDA=∠CAB.(注:三角形内角和等于180°)

(1)求证:∠CDA=∠DAB+∠DBA;
(2)如图2,MN是经过点D的一条直线,若直线MN交AC边于点E,且∠CDE=∠CAD.求证:∠AED+∠EAB=180°;
(3)将图2中的直线MN绕点D旋转,使它与射线AB交于点P(点P不与点A,B重合).在图3中画出直线MN,并用等式表示∠CAD,∠BDP,∠BPD这三个角之间的数量关系,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A,B两点,分别表示﹣40,20,甲、乙两只蚂蚁分别从A,B两点同时出发,甲沿线段AB方向以3个单位长度/秒的速度向右运动,甲到达点B处时运动停止;乙沿线段BA方向以5个单位长度/秒的速度向左运动.
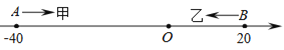
(1)求甲、乙第一次相遇点所表示的数.
(2)求经过多少秒时,甲、乙相距28个单位长度?
(3)若乙到达A点后立刻掉头追赶甲(速度保持不变),则在甲到达B点前,甲、乙是否还能再次相遇?若能,求出相遇点所表示的数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在数轴上有![]() 两点,点
两点,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 在
在![]() 点的左边,且
点的左边,且![]() .若有一动点
.若有一动点![]() 从数轴上点
从数轴上点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向左匀速运动,动点
个单位长度的速度沿数轴向左匀速运动,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单 位长度的速度沿着数轴向右匀速运动,设运动时间为
个单 位长度的速度沿着数轴向右匀速运动,设运动时间为![]() 秒,解决以下问题:
秒,解决以下问题:
![]() 写出数轴上点
写出数轴上点![]() 所表示的数;
所表示的数;
![]() 若点
若点![]() 分别从
分别从![]() 两点同时出发,问点
两点同时出发,问点![]() 运动多少秒与点
运动多少秒与点![]() 相距
相距![]() 个单位长度?
个单位长度?
![]() 探索问题:若
探索问题:若![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,当点
的中点,当点![]() 在线段
在线段![]() 上运动过程中,探索线段
上运动过程中,探索线段![]() 与线段
与线段![]() 的数量关系(写出过程).
的数量关系(写出过程).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com