
【题目】如图,在直角坐标系xOy中,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点.
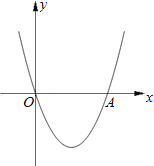
(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;
(3)对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由.
【答案】解:(1)∵函数的图象与x轴相交于O,∴0=k+1,∴k=﹣1。
∴这个二次函数的解析式为y=x2﹣3x。
(2)如图,过点B做BD⊥x轴于点D,
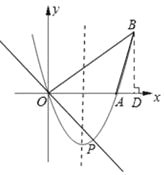
令x2﹣3x=0,解得:x=0或3。∴AO=3。
∵△AOB的面积等于6,∴![]() AOBD=6。∴BD=4。
AOBD=6。∴BD=4。
∵点B在函数y=x2﹣3x的图象上,
∴4=x2﹣3x,解得:x=4或x=﹣1(舍去)。
又∵顶点坐标为:( 1.5,﹣2.25),且2.25<4,
∴x轴下方不存在B点。
∴点B的坐标为:(4,4)。
(3)存在。
∵点B的坐标为:(4,4),∴∠BOD=45°,![]() 。
。
若∠POB=90°,则∠POD=45°。
设P点坐标为(x,x2﹣3x)。
∴![]() 。
。
若![]() ,解得x=4 或x=0(舍去)。此时不存在点P(与点B重合)。
,解得x=4 或x=0(舍去)。此时不存在点P(与点B重合)。
若![]() ,解得x=2 或x=0(舍去)。
,解得x=2 或x=0(舍去)。
当x=2时,x2﹣3x=﹣2。
∴点P 的坐标为(2,﹣2)。
∴![]() 。
。
∵∠POB=90°,∴△POB的面积为:![]() POBO=
POBO=![]() ×
×![]() ×
×![]() =8。
=8。
【解析】(1)将原点坐标代入抛物线中即可求出k的值,从而求得抛物线的解析式。
(2)根据(1)得出的抛物线的解析式可得出A点的坐标,也就求出了OA的长,根据△OAB的面积可求出B点纵坐标的绝对值,然后将符合题意的B点纵坐标代入抛物线的解析式中即可求出B点的坐标,然后根据B点在抛物线对称轴的右边来判断得出的B点是否符合要求即可。
(3)根据B点坐标可求出直线OB的解析式,由于OB⊥OP,由此可求出P点的坐标特点,代入二次函数解析式可得出P点的坐标.求△POB的面积时,求出OB,OP的长度即可求出△BOP的面积。


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3交x轴于A,B两点,交y轴于点C,点D为抛物线的顶点,点C关于抛物线的对称轴的对称点为E,点G,F分别在x轴和y轴上,则四边形EDFG周长的最小值为_____.
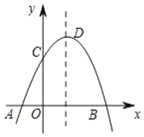
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为6,则k的值为_____.
(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为6,则k的值为_____.
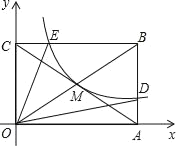
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是圆O直径CA延长线上的一点,PB切圆O于点B,点D是圆上的一点,连接AB,AD,BD,CD,PB=BC.
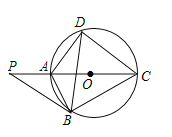
(1)求证:OP=2OC;
(2)若OC=5,sin∠DCA=![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线y=kx+b(k,b为常数)分别与x轴、y轴交于点A(﹣4,0),B(0,3),抛物线y=﹣x2+4x+1与y轴交于点C,点E在抛物线y=﹣x2+4x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( )
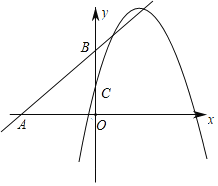
A.2B.4C.2.5D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线y=﹣x2+2mx﹣m2+m.
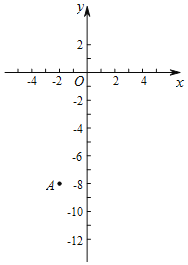
(1)求抛物线的对称轴(用含m的式子表示);
(2)如果该抛物线的顶点在直线y=2x﹣4上,求m的值.
(3)点A的坐标为(﹣2,﹣8),点A关于点(0,﹣9)的对称点为B点.
①写出点B坐标.
②若该抛物线与线段AB有公共点,结合函数图象,直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com