
【题目】如图,对称轴为直线x=-1的抛物线y=a(x-h)![]() -4(a≠0)与x轴相交于A、B两点,与y轴交于点C,其中点A的坐标为(-3,0).
-4(a≠0)与x轴相交于A、B两点,与y轴交于点C,其中点A的坐标为(-3,0).
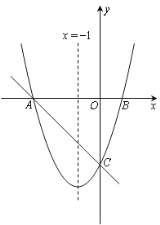
(1)求该抛物线的解析式;
(2)若点P在抛物线上,且S△POC=4S△BOC.求点P的坐标;
(3)设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
【答案】(1)所求抛物线的解析式是![]() ;
;
(2)点![]() 的坐标为
的坐标为![]() ,或
,或![]() ;
;
(3)如当![]() 时,
时,![]() 有最大值
有最大值![]() .
.
【解析】
(1)因为抛物线的对称轴为![]() ,可得h值;
,可得h值;![]() 点坐标为
点坐标为![]() 在抛物线上,代入抛物线的解析式,即可解答;
在抛物线上,代入抛物线的解析式,即可解答;
(2)先由二次函数的解析式为![]() ,得到
,得到![]() 点坐标,然后设
点坐标,然后设![]() 点坐标为
点坐标为![]() ,根据
,根据![]() 列出关于
列出关于![]() 的方程,解方程求出
的方程,解方程求出![]() 的值,进而得到点
的值,进而得到点![]() 的坐标;
的坐标;
(3)先运用待定系数法求出直线![]() 的解析式为
的解析式为![]() ,再设
,再设![]() 点坐标为
点坐标为![]() ,则
,则![]() 点坐标为
点坐标为![]() ,然后用含
,然后用含![]() 的代数式表示
的代数式表示![]() ,根据二次函数的性质即可求出线段
,根据二次函数的性质即可求出线段![]() 长度的最大值.
长度的最大值.
(1)由题意对称轴为直线![]() ,
,
设抛物线解析式为![]() ,把点
,把点![]() 代入得
代入得![]() ,
,
![]() .
.
∴所求抛物线的解析式是![]() .
.
(2)如图1.
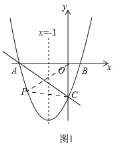
![]() ,当
,当![]() 时,
时,![]() .所以点
.所以点![]() ,
,![]() .
.
令![]() ,解得
,解得![]() ,或
,或![]() .
.![]() 点
点![]() ,
,![]() .
.
设点![]() .
.
此时![]() .
.
![]() .
.
由![]() 得
得![]() .
.
解得![]() 或
或![]() .
.
所以![]() 或
或![]() .
.
所以点![]() 的坐标为
的坐标为![]() ,或
,或![]() .
.
(3)如图2.
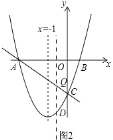
设直线![]() 的解析式为:
的解析式为:![]() .
.
把![]() ,
,![]() 代入得
代入得![]() ,解得
,解得![]() .
.
所以直线AC的解析式为![]() .
.
设点![]() ,点
,点![]() .
.
所以![]() .
.
所以当![]() 时,
时,![]() 有最大值
有最大值![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=ax2+bx+c的图象如图所示,那么关于x的一元二次方程ax2+bx+c-3=0的根的情况是( )
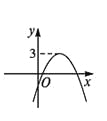
A. 有两个不相等的实数根
B. 有两个异号的实数根
C. 有两个相等的实数根
D. 没有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
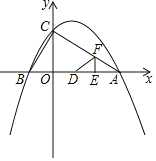
已知二次函数y=﹣![]() x2+
x2+![]() x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)求证:△ABC为直角三角形;
(3)如图,动点E,F同时从点A出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒![]() 个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
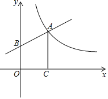
【题目】如图,已知点A在反比例函数![]() (x>0)的图像上,过点A作AC⊥x轴,垂足是C,AC=OC.一次函数y=kx+b的图像经过点A,与y轴的正半轴交于点B.
(x>0)的图像上,过点A作AC⊥x轴,垂足是C,AC=OC.一次函数y=kx+b的图像经过点A,与y轴的正半轴交于点B.
(1)求点A的坐标;
(2)若四边形ABOC的面积是![]() ,求一次函数y=kx+b的表达式.
,求一次函数y=kx+b的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
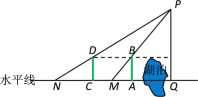
【题目】我国古代数学家刘徽发展了“重差术”,用于测量不可到达的物体的高度,比如,通过下列步骤可测量山的高度PQ(如图):
(1)测量者在水平线上的A处竖立一根竹竿,沿射线QA方向走到M处,测得山顶P、竹竿顶端B及M在一条直线上;
(2)将该竹竿竖立在射线QA上的C处,沿原方向继续走到N处,测得山顶P、竹竿顶端D及N在一条直线上;
(3)设竹竿与AM、CN的长分别为![]() 、a1、a2,可得公式:PQ=
、a1、a2,可得公式:PQ=![]() +
+![]() .则上述公式中,d表示的是( )
.则上述公式中,d表示的是( )
A. QA的长 B. AC的长 C. MN的长 D. QC的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com