
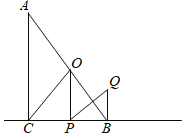
【题目】如图所示,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与B、C重合),连接OC、OP,将OP绕点P顺时针旋转60°,得到线段PQ,连接BQ,若∠BPO=15°,BP=4,则BQ的长为_____.
【答案】2+2![]() 或4
或4![]() ﹣4
﹣4
【解析】
分两种情况:①当点P在CB延长线上时,连接OQ,证得△OBC是等边三角形得出![]() ,由旋转的性质得出△OPQ是等边三角形,得出
,由旋转的性质得出△OPQ是等边三角形,得出![]() ,推出
,推出![]() ,由SAS证得
,由SAS证得![]() 得出
得出![]() ,证得
,证得![]() ,过点P作PD⊥BQ于D,则
,过点P作PD⊥BQ于D,则![]() ,由勾股定理得出
,由勾股定理得出![]() ,证得△QDP是等腰直角三角形得出
,证得△QDP是等腰直角三角形得出![]() ,则
,则![]() ;
;
②当点P在BC延长线上时,连接OQ,证得△OBC是等边三角形得出![]() ,推出
,推出![]() ,由旋转的性质得出△OPQ是等边三角形得出
,由旋转的性质得出△OPQ是等边三角形得出![]() ,推出
,推出![]() ,由SAS证得
,由SAS证得![]() 得出
得出![]() ,证得
,证得![]() ,过点Q作QE⊥BP于E,则
,过点Q作QE⊥BP于E,则![]() ,设
,设![]() ,则
,则![]() ,由勾股定理得出
,由勾股定理得出![]() ,由等腰直角三角形的性质得出
,由等腰直角三角形的性质得出![]() ,则
,则![]() ,求解即可得出答案.
,求解即可得出答案.
依题意,分以下两种情况:
①如图1,当点P在CB延长线上时,连接OQ
![]() 中,点O为AB中点
中,点O为AB中点
![]()
![]()
![]()
∴△OBC是等边三角形
![]()
∵OP绕点P顺时针旋转![]() ,得到线段PQ
,得到线段PQ
∴△OPQ是等边三角形
![]()
![]()
在△COP和△BOQ中,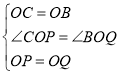
![]()
![]()
![]()
![]()
过点P作PD⊥BQ于D,则![]()
![]()
![]()
∴△QDP是等腰直角三角形
![]()
![]() ;
;
②如图2,当点P在BC延长线上时,连接OQ
![]() 中,点O为AB中点
中,点O为AB中点
![]()
![]()
![]()
∴△OBC是等边三角形
![]()
![]()
∵OP绕点P顺时针旋转![]() ,得到线段PQ
,得到线段PQ
∴△OPQ是等边三角形
![]()
![]()
在△COP和△BOQ中,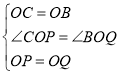
![]()
![]()
![]()
![]()
![]()
过点Q作QE⊥BP于E,则![]()
设![]() ,则
,则![]()
![]()
![]()
![]()
![]()
解得![]() ,即
,即![]()
综上,BQ的长为![]() 或
或![]()
故答案为:![]() 或
或![]() .
.



 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
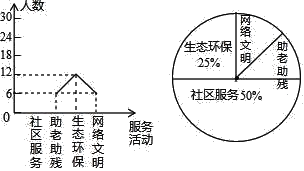
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,合肥市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)请把折线统计图补充完整;
(2)求扇形统计图中,网络文明部分对应的圆心角的度数;
(3)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,将它的纵坐标
,将它的纵坐标![]() 与横坐标
与横坐标![]() 的比
的比![]() 称为点
称为点![]() 的“理想值”,记作
的“理想值”,记作![]() .如
.如![]() 的“理想值”
的“理想值”![]() .
.
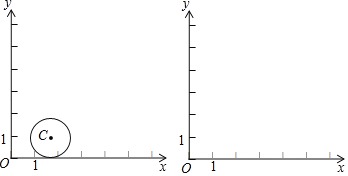
(1)①若点![]() 在直线
在直线![]() 上,则点
上,则点![]() 的“理想值”
的“理想值”![]() 等于_______;
等于_______;
②如图,![]() ,
,![]() 的半径为1.若点
的半径为1.若点![]() 在
在![]() 上,则点
上,则点![]() 的“理想值”
的“理想值”![]() 的取值范围是_______.
的取值范围是_______.
(2)点![]() 在直线
在直线![]() 上,
上,![]() 的半径为1,点
的半径为1,点![]() 在
在![]() 上运动时都有
上运动时都有![]() ,求点
,求点![]() 的横坐标
的横坐标![]() 的取值范围;
的取值范围;
(3)![]() ,
,![]() 是以
是以![]() 为半径的
为半径的![]() 上任意一点,当
上任意一点,当![]() 时,画出满足条件的最大圆,并直接写出相应的半径
时,画出满足条件的最大圆,并直接写出相应的半径![]() 的值.(要求画图位置准确,但不必尺规作图)
的值.(要求画图位置准确,但不必尺规作图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级6班的一个互助学习小组组长收集并整理了组员们讨论如下问题时所需的条件.如图所示,在四边形![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,____________________.求证:四边形
上,____________________.求证:四边形![]() 是平行四边形.你能在横线上填上最少且简捷的条件使结论成立吗?条件分别是:①
是平行四边形.你能在横线上填上最少且简捷的条件使结论成立吗?条件分别是:①![]() ;②
;②![]() ;③
;③![]() ;④四边形
;④四边形![]() 是平行四边形,其中A、B、C、D四位同学所填条件符合题目要求的是( )
是平行四边形,其中A、B、C、D四位同学所填条件符合题目要求的是( )
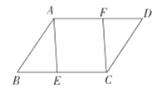
A.①②B.①②③C.①④D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
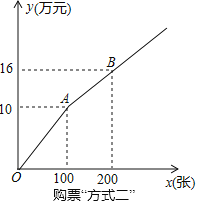
【题目】世界500强H公司决定购买某演唱会门票奖励部分优秀员工,演唱会的购票方式有以下两种,
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元(其中总费用=广告赞助费+门票费);
方式二:如图所示,设购买门票x张,总费用为y万元
(1)求用购票“方式一”时y与x的函数关系式;
(2)若H、A两家公司分别釆用方式一、方式二购买本场演唱会门票共400张,且A公司购买超过100张,两公司共花费27.2万元,求H、A两公司各购买门票多少张?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形![]() 中,
中,![]() 在
在![]() 上从
上从![]() 向
向![]() 运动,连接
运动,连接![]() 交
交![]() 于
于![]() 连接
连接![]() .
.
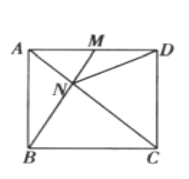
(1)证明:无论![]() 运动到
运动到![]() 上的何处,都有
上的何处,都有![]() ;
;
(2)当![]() 运动到何处时,
运动到何处时,![]() ?
?
(3)若![]() 从
从![]() 到
到![]() 再从
再从![]() 到
到![]() ,在整个运动过程中,
,在整个运动过程中,![]() 为多少时,
为多少时,![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△AOB是等腰直角三角形,∠AOB=90°,点A(2,1).
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的函数表达式;
(3)在(2)所求的抛物线上,是否存在一点P,使四边形ABOP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C,D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为______.
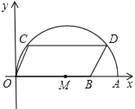
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() 的三个顶点坐标分别是
的三个顶点坐标分别是![]() ,
,![]() ,
,![]() .
.
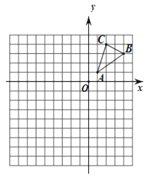
(1)请作出![]() 绕
绕![]() 点逆时针旋转
点逆时针旋转![]() 的
的![]() ;
;
(2)以点![]() 为位似中心,将
为位似中心,将![]() 扩大为原来的2倍,得到
扩大为原来的2倍,得到![]() ,请在
,请在![]() 轴的左侧画出
轴的左侧画出![]() ;
;
(3)请直接写出![]() 的正弦值.
的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com